Shannon-Fanovo kódování: Porovnání verzí

Řádek 84: Řádek 84:
 
|-
 
|-
 
| E || 1
 
| E || 1
−
|}                                                                   [[File:1.PNG|200px]]
+
|}                                               [[File:1.PNG|200px]]
 
'''''Krok 2''''' = Nyní oba seznamy rozdělit na poloviny s přibližně stejným součtem četostí
 
'''''Krok 2''''' = Nyní oba seznamy rozdělit na poloviny s přibližně stejným součtem četostí
 
{| class="wikitable"
 
{| class="wikitable"
Řádek 101: Řádek 101:
 
|-
 
|-
 
| E || 1 '''1'''
 
| E || 1 '''1'''
−
|}    
+
|}                                               [[File:2.PNG|200px]]
−
 
+
'''''Krok 3''''' = Seznamy (F) a (D) již rozložit nejdou, zbývá zpracovat seznamy (C,A) a (B,E). Opět oba rozložit na poloviny s přibližně stejným součtem četností.
 +
{| class="wikitable"
 +
|-
 +
! Symbol !! Kód
 +
|-
 +
| F || 0 0
 +
|-
 +
| D || 0 1
 +
|-
 +
| C || 1 0 '''0'''
 +
|-
 +
| A || 1 0 '''1'''
 +
|-
 +
| B || 1 1 '''0'''
 +
|-
 +
| E || 1 1 '''1'''
 +
|}                          [[File:3.PNG|200px]]
 +
'''''Výsledek'''''                               
 +
{| class="wikitable"
 +
|-
 +
! Symbol !! Kód
 +
|-
 +
| F || 0 0
 +
|-
 +
| D || 0 1
 +
|-
 +
| C || 1 0 0
 +
|-
 +
| A || 1 0 1
 +
|-
 +
| B || 1 1 0
 +
|-
 +
| E || 1 1 1
 +
|}[http://voho.eu/wiki/kodovani-shannon-fano/]
 
2)
 
2)
 
* Vstupní soubor: ABRAKADABRA
 
* Vstupní soubor: ABRAKADABRA

Verze z 19. 12. 2018, 10:28

Základní popis

Shannon-Fanovo kódování je technika pro sestavení prefixového kódu založená na seznamu symbolů a počtech jejich výskytů. v roce 1949 metodu nezávisle na sobě publikovali Claude Elwood Shannon (otec teorie informace)[1] s Warrenem Weaverem a Robertem Mario Fano.[2]

  • Řešení nemusí být vždy optimální (nejkratší)
  • Používá se v kompresních datech [3]
  • Asymetrická kompresní metoda
  • Dvouprůchodová kompresní metoda
  • Semi-adaptivní kompresní metoda
  • Dosahuje horších výsledků ve srovnání s Huffmanovým kódováním[4]
                                                                            C.E.Shannon C.E.Shannon [5]

Konstrukce binárního kódu

Princip

Princip je založen na množině znaků rekursivně dělících se vždy na dvě podmnožiny, aby součet výskytů znaků v obou podmnožinách byl přibližně stejný. Jedné podmnožině je pak v kódu přiřazena binární 1 a druhé 0.[6]

  • Postup není optimální
  • Důležitá vlastnost: opětovné prefixovost


Prefixovost Shannon-Fanova kódu můžeme zachytit binárním prefixovým stromem. Písmena vstupní abecedy jsou v listech a jejich kódy tvoří od cesta od kořene do daného vrcholu.

  • Neprefixový kód = na cestě do nějakého listu leží nějaké písmeno vstupní abecedy[7]

Pseudokód

  1. Pro danou zprávu vytvořit seznam symbolů a zjistit počet jejich výskytů (nebo pravděpodobnost)
  2. Seznam symbolů seřadit do neklesající posloupnosti podle této hodnoty
  3. Kódy všech symbolů jsou zpočátku prázdné
  4. Rozdělit seznam na dvě poloviny tak, aby součet sledovaných hodnot byl v obou částech zhruba stejný
  5. Ke kódům symbolů levé polovině připojit 0, ke kódům symbolů v pravé polovině připojit 1
  6. Rekurzivně opakovat od kroku 4 na levou i pravou polovinu seznamu [8]

Příklad

1)

Symbol Počet výskytů
F 5
D 4
C 4
A 3
B 3
E 2

Inicializace Seznam je (F,D,C,A,B,E). Kódy všech symbolů jsou prázdné.

Symbol Kód
F -
D -
C -
A -
B -
E -

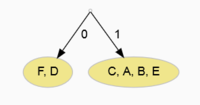
Krok 1 = Rozdělit na dvě poloviny s přibližně stejným součtem četností

  • (F,D) - součet četností: 5 + 4 = 9
  • (C,A,B,E) - součet četností: 4 + 3 + 3 + 2 = 12
Symbol Kód
F 0
D 0
C 1
A 1
B 1
E 1

1.PNG

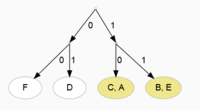
Krok 2 = Nyní oba seznamy rozdělit na poloviny s přibližně stejným součtem četostí

Symbol Kód
F 0 0
D 0 1
C 1 0
A 1 0
B 1 1
E 1 1

2.PNG

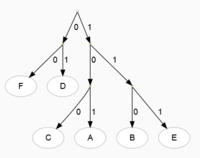
Krok 3 = Seznamy (F) a (D) již rozložit nejdou, zbývá zpracovat seznamy (C,A) a (B,E). Opět oba rozložit na poloviny s přibližně stejným součtem četností.

Symbol Kód
F 0 0
D 0 1
C 1 0 0
A 1 0 1
B 1 1 0
E 1 1 1

3.PNG

Výsledek

Symbol Kód
F 0 0
D 0 1
C 1 0 0
A 1 0 1
B 1 1 0
E 1 1 1

[9]

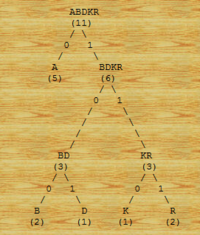
2)

  • Vstupní soubor: ABRAKADABRA
  • Jednotlivé znaky: A B D K R
  • Počty výskytů: (5) (2) (1) (1) (2)
  • Vytvořený strom:

Strom.PNG[10]

Citováno z „https://wikisofia.cz/w/index.php?title=Shannon-Fanovo_kódování&oldid=56492“