Korelační a regresní analýza: Porovnání verzí
m |
|||
| (Není zobrazeno 5 mezilehlých verzí od stejného uživatele.) | |||
| Řádek 1: | Řádek 1: | ||
== Korelace == | == Korelace == | ||
| + | |||
* Znázorňuje statistickou závislost dvou kvantitativních veličin (měří vzájemný vztah dvou proměnných. | * Znázorňuje statistickou závislost dvou kvantitativních veličin (měří vzájemný vztah dvou proměnných. | ||
* Dvě proměnné jsou korelované, jestliže určité hodnoty jedné proměnné mají tendenci se vyskytovat společně s určitými hodnotami druhé proměnné<ref>Hendl, J. (2009). Přehled statistických metod: Analýza a metaanalýza dat. Praha: Portál</ref> | * Dvě proměnné jsou korelované, jestliže určité hodnoty jedné proměnné mají tendenci se vyskytovat společně s určitými hodnotami druhé proměnné<ref>Hendl, J. (2009). Přehled statistických metod: Analýza a metaanalýza dat. Praha: Portál</ref> | ||
| + | |||
=== Korelační koeficienty === | === Korelační koeficienty === | ||
| + | |||
Vlastnosti ''korelačního koeficientu r'': | Vlastnosti ''korelačního koeficientu r'': | ||
* Označujeme ''r'' | * Označujeme ''r'' | ||
| Řádek 10: | Řádek 13: | ||
* ''r = -1'' ⇒ nepřímá závislost | * ''r = -1'' ⇒ nepřímá závislost | ||
Korelační determinace r<sup>2</sup> – znázorňuje podíl společné variance | Korelační determinace r<sup>2</sup> – znázorňuje podíl společné variance | ||
| + | |||
==== Pearsonův korelační koeficient ==== | ==== Pearsonův korelační koeficient ==== | ||
| − | * Měří statistickou závislost u lineárních dat | + | |
| + | * Měří statistickou závislost u lineárních dat (je parametrický) | ||
* Korelační koeficient je velmi ovlivněn odlehlými hodnotami | * Korelační koeficient je velmi ovlivněn odlehlými hodnotami | ||
* Korelační koeficient se počítá pomocí směrodatných odchylek obou proměnných a jejich kovariance (''kovariance'' = míra vzájemné vazby mezi veličinami) | * Korelační koeficient se počítá pomocí směrodatných odchylek obou proměnných a jejich kovariance (''kovariance'' = míra vzájemné vazby mezi veličinami) | ||
| − | <math>r=\frac{\sum\left(x_i-x̄ \right)\left(y_i-y \right)}{\sqrt{\sum\left(x_i- | + | <math>r=\frac{\sum\left(x_i-x̄ \right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\left(x_i-\bar{x}\right)^2\sum\left(y_i-\bar{y}\right)^2}}=\frac{S_{xy}}{S_x S_y}</math> |
==== Spearmanův koeficient korelace ==== | ==== Spearmanův koeficient korelace ==== | ||
| + | |||
* Označujeme r<sub>sp</sub> | * Označujeme r<sub>sp</sub> | ||
| − | * Korelační koeficient pořadí | + | * Korelační koeficient pořadí (neparametrická metoda) |
| − | * Zachycuje obecně monotónní (rostoucí/ klesající) vztahy mezi proměnnými, nikoli pouze lineární | + | * Zachycuje obecně monotónní (rostoucí/ klesající) vztahy mezi proměnnými, nikoli pouze lineární |
| − | * Je rezistentní vůči odlehlým hodnotám | + | * Je rezistentní vůči odlehlým hodnotám |
| − | * Pro malé rozsahy dat je jeho výpočet méně pracný než Pearsonův korelační koeficient | + | * Pro malé rozsahy dat je jeho výpočet méně pracný než Pearsonův korelační koeficient |
| − | <math>r_{sp}=1-\frac{6\sum | + | <math>r_{sp}=1-\frac{6\sum DIF^2}{n(n^2-1)}</math> |
==== Kendallův korelační koeficient ==== | ==== Kendallův korelační koeficient ==== | ||
| − | * Označujeme tau t<sub>k</sub | + | |
| − | * Neparametrický test nezávislosti | + | * Označujeme tau t<sub>k</sub> |
| − | * Rozdíl mezi pravděpodobností, že hodnoty dvou proměnných jsou ve stejném pořadí, a pravděpodobností, že ve stejném pořadí nejsou | + | * Neparametrický test nezávislosti |
| − | * Větší citlivost na některé nelineární vztahy | + | * Rozdíl mezi pravděpodobností, že hodnoty dvou proměnných jsou ve stejném pořadí, a pravděpodobností, že ve stejném pořadí nejsou |
| + | * Větší citlivost na některé nelineární vztahy | ||
| + | |||
==== Čtyřpolní korelační koeficient ==== | ==== Čtyřpolní korelační koeficient ==== | ||
| − | * Označujeme φ | + | |
| − | * Jedná se o Pearsonův korelační koeficient vypočítaný pro dvě alternativní proměnné, které kódujeme pomocí hodnot 0 a 1 | + | * Označujeme φ |
| + | * Jedná se o Pearsonův korelační koeficient vypočítaný pro dvě alternativní proměnné, které kódujeme pomocí hodnot 0 a 1 | ||
| + | |||
==== Bodově biserální koeficient korelace ==== | ==== Bodově biserální koeficient korelace ==== | ||
| − | * Označujeme r<sub>pb</sub | + | |
| − | * Měří vztah mezi spojitou metrickou proměnnou a binární proměnnou | + | * Označujeme r<sub>pb</sub> |
| + | * Měří vztah mezi spojitou metrickou proměnnou a binární proměnnou | ||
* V praxi se vzorec zpravidla nepoužívá (lze jej nahradit použitím algoritmu pro Pearsonův koeficient korelace, kde binární proměnnou zastupují nuly a jedničky) | * V praxi se vzorec zpravidla nepoužívá (lze jej nahradit použitím algoritmu pro Pearsonův koeficient korelace, kde binární proměnnou zastupují nuly a jedničky) | ||
| − | + | ||
=== Příklady využití korelačních koeficientů v psychometrii === | === Příklady využití korelačních koeficientů v psychometrii === | ||
| − | * Reliabilita (korelace test – retest, split half) | + | |
| − | * Validita (korelace test – kritérium) | + | * [[Reliabilita]] (korelace test – retest, split half) |
| − | * Diskriminační síla položky (korelace položka – test) | + | * [[Validita]] (korelace test – kritérium) |
| − | * Odhad objektivity (korelace hodnotitel I – hodnotitel II) | + | * Diskriminační síla položky (korelace položka – test) |
| + | * Odhad objektivity (korelace hodnotitel I – hodnotitel II) | ||
| + | |||
== Regresní analýza == | == Regresní analýza == | ||
| + | |||
Regresní analýza je statistická metoda, umožňující nám prozkoumat vztah mezi dvěma proměnnými - tzv. '''nezávisle proměnnou''' (X – nazýváme regresand, cílová proměnná) a tzv. '''závisle proměnnou''' (Y – nazýváme též regresor)<ref>Hendl, J. (2006). Přehled statistických metod zpracování dat. Praha: Portál.</ref><ref>Zvára, K. (2008). Regresní analýza. Praha: Matfypress.</ref><ref>Regresní analýza. Retrieved from: http://cs.wikipedia.org/wiki/Regresní_analýza </ref>. Pomáhá nám pochopit, jak se změní hodnota závisle proměnné v návaznosti na změnu jedné z nezávisle proměnných (zatímco ostatní nezávisle proměnné zůstávají konstantní). Konečný odhad je založen na tzv. '''regresní funkci'''.<br /> | Regresní analýza je statistická metoda, umožňující nám prozkoumat vztah mezi dvěma proměnnými - tzv. '''nezávisle proměnnou''' (X – nazýváme regresand, cílová proměnná) a tzv. '''závisle proměnnou''' (Y – nazýváme též regresor)<ref>Hendl, J. (2006). Přehled statistických metod zpracování dat. Praha: Portál.</ref><ref>Zvára, K. (2008). Regresní analýza. Praha: Matfypress.</ref><ref>Regresní analýza. Retrieved from: http://cs.wikipedia.org/wiki/Regresní_analýza </ref>. Pomáhá nám pochopit, jak se změní hodnota závisle proměnné v návaznosti na změnu jedné z nezávisle proměnných (zatímco ostatní nezávisle proměnné zůstávají konstantní). Konečný odhad je založen na tzv. '''regresní funkci'''.<br /> | ||
Velmi vděčni za regresní analýzu budeme ve chvíli, kdy se např. rozhodneme k posouzení kvalit uchazečů o zaměstnání použít testovou baterii 3 testů. Zatímco korelační koeficient nám umožní zjistit, zda mezi proměnnými existuje vztah a jak je silný (to znamená, zda zvolené testy korelují např. s hodnocením, jaké zaměstnanec získá po ukončení zkušební doby), regresní analýza postupuje o krok dál a umožní nám na základě získaných dat predikovat do budoucna. (V tomto případě tak díky regresní analýze můžeme zjistit, že ačkoliv všechny tři zvolené testy vysoce korelují s kritériem, už pouhý jeden ze zvolených tesů má pro nás dostatečnou predikční sílu a v budoucnu tak využijeme jen tento jeden a uspoříme tak čas). | Velmi vděčni za regresní analýzu budeme ve chvíli, kdy se např. rozhodneme k posouzení kvalit uchazečů o zaměstnání použít testovou baterii 3 testů. Zatímco korelační koeficient nám umožní zjistit, zda mezi proměnnými existuje vztah a jak je silný (to znamená, zda zvolené testy korelují např. s hodnocením, jaké zaměstnanec získá po ukončení zkušební doby), regresní analýza postupuje o krok dál a umožní nám na základě získaných dat predikovat do budoucna. (V tomto případě tak díky regresní analýze můžeme zjistit, že ačkoliv všechny tři zvolené testy vysoce korelují s kritériem, už pouhý jeden ze zvolených tesů má pro nás dostatečnou predikční sílu a v budoucnu tak využijeme jen tento jeden a uspoříme tak čas). | ||
| + | |||
=== Historie === | === Historie === | ||
| + | |||
Pojem regrese (z lat. ''regressus'', ustupuji, pohybuji se zpět) zavedl do statistiky anglický vědec [[Francis Galton]] koncem 19.století, a to jako "''regres(i) k průměru''". Tím označil fakt, že např. synové vysokých rodičů jsou sice v průměru (statisticky) vyšší než byli jejich rodiče, zároveň ale individuálně nedosahují extrémních hodnot předchozí generace. Jako kdyby se jedinci postupně "vraceli k průměru". Galtonův název se z jeho eugenických výzkumů rozšířil na jakékoli zkoumání souvislostí mezi náhodnými veličinami a vznikla statistická regresní analýza. | Pojem regrese (z lat. ''regressus'', ustupuji, pohybuji se zpět) zavedl do statistiky anglický vědec [[Francis Galton]] koncem 19.století, a to jako "''regres(i) k průměru''". Tím označil fakt, že např. synové vysokých rodičů jsou sice v průměru (statisticky) vyšší než byli jejich rodiče, zároveň ale individuálně nedosahují extrémních hodnot předchozí generace. Jako kdyby se jedinci postupně "vraceli k průměru". Galtonův název se z jeho eugenických výzkumů rozšířil na jakékoli zkoumání souvislostí mezi náhodnými veličinami a vznikla statistická regresní analýza. | ||
| + | |||
=== Lineární regresní funkce === | === Lineární regresní funkce === | ||
| + | |||
Lineární regrese je metoda, při které je soubor bodů v grafu proložen přímkou, neboť předpokládáme, že závislost ''y'' na ''x'' lze graficky vyjádřit přímkou (viz. obrázek). Pokud měřené body proložíme přímkou, bude při odečítání z grafu mezi ypsilonovou hodnotou měřeného bodu a ypsilonovou hodnotou ležící na vytvoření přímce odchylka. Podstatou lineární regrese je nalézt právě takovou přímku, aby součet druhých mocnin zmíněných odchylek byl co nejmenší, jedná se tedy o aproximaci daných hodnot přímkou a to metodou nejmenších čtverců. | Lineární regrese je metoda, při které je soubor bodů v grafu proložen přímkou, neboť předpokládáme, že závislost ''y'' na ''x'' lze graficky vyjádřit přímkou (viz. obrázek). Pokud měřené body proložíme přímkou, bude při odečítání z grafu mezi ypsilonovou hodnotou měřeného bodu a ypsilonovou hodnotou ležící na vytvoření přímce odchylka. Podstatou lineární regrese je nalézt právě takovou přímku, aby součet druhých mocnin zmíněných odchylek byl co nejmenší, jedná se tedy o aproximaci daných hodnot přímkou a to metodou nejmenších čtverců. | ||
[[Soubor:Regresni-analyza.png|Model regresní analýzy]] | [[Soubor:Regresni-analyza.png|Model regresní analýzy]] | ||
| + | |||
<small>'''Model regresní analýzy'''<br /> | <small>'''Model regresní analýzy'''<br /> | ||
V rovnici lineární regresní model vyjádříme takto '''y = α + βx + e''', přičemž ''β'' představuje vektor, α bod, ve kterém vložená přímka protíná ypsilonovou osu, ''x'' představuje nezávisle proměnnou, ''y'' představuje závisle proměnnou a ''e'' představuje chybu.<br /> | V rovnici lineární regresní model vyjádříme takto '''y = α + βx + e''', přičemž ''β'' představuje vektor, α bod, ve kterém vložená přímka protíná ypsilonovou osu, ''x'' představuje nezávisle proměnnou, ''y'' představuje závisle proměnnou a ''e'' představuje chybu.<br /> | ||
Neznámé hodnoty α a β odhadujeme právě pomocí metody nejmenších čtverců.</small> | Neznámé hodnoty α a β odhadujeme právě pomocí metody nejmenších čtverců.</small> | ||
| + | |||
==== Postup v SPSS ==== | ==== Postup v SPSS ==== | ||
| + | |||
'''Zadání výpočtu''' | '''Zadání výpočtu''' | ||
* Pro snadnější porozumění co a kam vyplnit použijeme následující příklad: Úspěšnost v prodeji nahrávky v závislosti na množství reklamy (vyjádřeno ve finanční nákladnosti reklamy)<ref>Field, A. (2007). Discovering Statistics Using IBM SPSS Statistics. Londýn: SAGE.</ref>. | * Pro snadnější porozumění co a kam vyplnit použijeme následující příklad: Úspěšnost v prodeji nahrávky v závislosti na množství reklamy (vyjádřeno ve finanční nákladnosti reklamy)<ref>Field, A. (2007). Discovering Statistics Using IBM SPSS Statistics. Londýn: SAGE.</ref>. | ||
| Řádek 74: | Řádek 95: | ||
## Na základě čísel získaných v této tabulce mohu předvídat prodej nahrávek dle objemu investovaných peněz do reklamy podle této „rovnice“ | ## Na základě čísel získaných v této tabulce mohu předvídat prodej nahrávek dle objemu investovaných peněz do reklamy podle této „rovnice“ | ||
## Prodej nahrávky = „intercept“ + (sklon x finanční investice do reklamy) | ## Prodej nahrávky = „intercept“ + (sklon x finanční investice do reklamy) | ||
| + | |||
== Zdroje == | == Zdroje == | ||
| + | |||
| + | === Reference === | ||
| + | |||
<references/> | <references/> | ||
Aktuální verze z 1. 6. 2016, 10:32
Korelace
- Znázorňuje statistickou závislost dvou kvantitativních veličin (měří vzájemný vztah dvou proměnných.
- Dvě proměnné jsou korelované, jestliže určité hodnoty jedné proměnné mají tendenci se vyskytovat společně s určitými hodnotami druhé proměnné[1]
Korelační koeficienty
Vlastnosti korelačního koeficientu r:
- Označujeme r
- r ∈ 〈-1,1〉
- r = 0 ⇒ nezávislost
- r = 1 ⇒ přímá závislost
- r = -1 ⇒ nepřímá závislost
Korelační determinace r2 – znázorňuje podíl společné variance
Pearsonův korelační koeficient
- Měří statistickou závislost u lineárních dat (je parametrický)
- Korelační koeficient je velmi ovlivněn odlehlými hodnotami
- Korelační koeficient se počítá pomocí směrodatných odchylek obou proměnných a jejich kovariance (kovariance = míra vzájemné vazby mezi veličinami)
Nelze pochopit (MathML, alternativně SVG nebo PNG (doporučeno pro moderní prohlížeče a kompenzační pomůcky): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r=\frac{\sum\left(x_i-x̄ \right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\left(x_i-\bar{x}\right)^2\sum\left(y_i-\bar{y}\right)^2}}=\frac{S_{xy}}{S_x S_y}}
Spearmanův koeficient korelace
- Označujeme rsp
- Korelační koeficient pořadí (neparametrická metoda)
- Zachycuje obecně monotónní (rostoucí/ klesající) vztahy mezi proměnnými, nikoli pouze lineární
- Je rezistentní vůči odlehlým hodnotám
- Pro malé rozsahy dat je jeho výpočet méně pracný než Pearsonův korelační koeficient
Kendallův korelační koeficient
- Označujeme tau tk
- Neparametrický test nezávislosti
- Rozdíl mezi pravděpodobností, že hodnoty dvou proměnných jsou ve stejném pořadí, a pravděpodobností, že ve stejném pořadí nejsou
- Větší citlivost na některé nelineární vztahy
Čtyřpolní korelační koeficient
- Označujeme φ
- Jedná se o Pearsonův korelační koeficient vypočítaný pro dvě alternativní proměnné, které kódujeme pomocí hodnot 0 a 1
Bodově biserální koeficient korelace
- Označujeme rpb
- Měří vztah mezi spojitou metrickou proměnnou a binární proměnnou
- V praxi se vzorec zpravidla nepoužívá (lze jej nahradit použitím algoritmu pro Pearsonův koeficient korelace, kde binární proměnnou zastupují nuly a jedničky)
Příklady využití korelačních koeficientů v psychometrii
- Reliabilita (korelace test – retest, split half)
- Validita (korelace test – kritérium)
- Diskriminační síla položky (korelace položka – test)
- Odhad objektivity (korelace hodnotitel I – hodnotitel II)
Regresní analýza
Regresní analýza je statistická metoda, umožňující nám prozkoumat vztah mezi dvěma proměnnými - tzv. nezávisle proměnnou (X – nazýváme regresand, cílová proměnná) a tzv. závisle proměnnou (Y – nazýváme též regresor)[2][3][4]. Pomáhá nám pochopit, jak se změní hodnota závisle proměnné v návaznosti na změnu jedné z nezávisle proměnných (zatímco ostatní nezávisle proměnné zůstávají konstantní). Konečný odhad je založen na tzv. regresní funkci.
Velmi vděčni za regresní analýzu budeme ve chvíli, kdy se např. rozhodneme k posouzení kvalit uchazečů o zaměstnání použít testovou baterii 3 testů. Zatímco korelační koeficient nám umožní zjistit, zda mezi proměnnými existuje vztah a jak je silný (to znamená, zda zvolené testy korelují např. s hodnocením, jaké zaměstnanec získá po ukončení zkušební doby), regresní analýza postupuje o krok dál a umožní nám na základě získaných dat predikovat do budoucna. (V tomto případě tak díky regresní analýze můžeme zjistit, že ačkoliv všechny tři zvolené testy vysoce korelují s kritériem, už pouhý jeden ze zvolených tesů má pro nás dostatečnou predikční sílu a v budoucnu tak využijeme jen tento jeden a uspoříme tak čas).
Historie
Pojem regrese (z lat. regressus, ustupuji, pohybuji se zpět) zavedl do statistiky anglický vědec Francis Galton koncem 19.století, a to jako "regres(i) k průměru". Tím označil fakt, že např. synové vysokých rodičů jsou sice v průměru (statisticky) vyšší než byli jejich rodiče, zároveň ale individuálně nedosahují extrémních hodnot předchozí generace. Jako kdyby se jedinci postupně "vraceli k průměru". Galtonův název se z jeho eugenických výzkumů rozšířil na jakékoli zkoumání souvislostí mezi náhodnými veličinami a vznikla statistická regresní analýza.
Lineární regresní funkce
Lineární regrese je metoda, při které je soubor bodů v grafu proložen přímkou, neboť předpokládáme, že závislost y na x lze graficky vyjádřit přímkou (viz. obrázek). Pokud měřené body proložíme přímkou, bude při odečítání z grafu mezi ypsilonovou hodnotou měřeného bodu a ypsilonovou hodnotou ležící na vytvoření přímce odchylka. Podstatou lineární regrese je nalézt právě takovou přímku, aby součet druhých mocnin zmíněných odchylek byl co nejmenší, jedná se tedy o aproximaci daných hodnot přímkou a to metodou nejmenších čtverců.
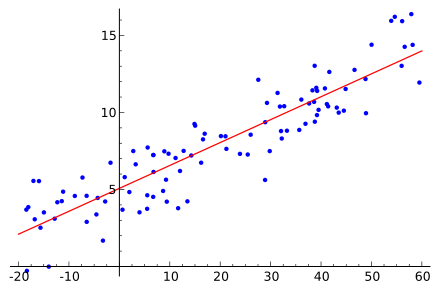
Model regresní analýzy
V rovnici lineární regresní model vyjádříme takto y = α + βx + e, přičemž β představuje vektor, α bod, ve kterém vložená přímka protíná ypsilonovou osu, x představuje nezávisle proměnnou, y představuje závisle proměnnou a e představuje chybu.
Neznámé hodnoty α a β odhadujeme právě pomocí metody nejmenších čtverců.
Postup v SPSS
Zadání výpočtu
- Pro snadnější porozumění co a kam vyplnit použijeme následující příklad: Úspěšnost v prodeji nahrávky v závislosti na množství reklamy (vyjádřeno ve finanční nákladnosti reklamy)[5].
- V menu SPSS postupně volíme Analyze → Regression → Linear…
- Nyní je potřeba vyplnit jednotlivá data a to následujícím způsobem
- Dependent variable – závislá proměnná, která graficky znázorněno leží na ose Y a jejíž vývoj chceme pomocí regrese předvídat z nezávisle proměnné (objem prodeje nahrávky)
- Independent variable – nezávisle proměnná, graficky znázorněno leží na ose Y (finanční investice do reklamy)
Interpretace dat:
- Tabulka: ignorujeme
- Tabulka MODEL SUMMARY:
- R = vyjádření prosté korelace mezi proměnnými
- R2 = toto číslo vynásobeno 100 je procento, do jaké míry nezávisle proměnná (reklama) vysvětluje pohyb (v našem případě nárůst) závisle proměnné (v našem případě prodej nahrávek)
- Tabulka ANOVA
- Zajímají nás hodnoty F a Sig pro účely zamítnutí nebo přijetí H0
- Tato tabulka vyjadřuje „pouze“ zda je náš model signifikantně dobrým predátorem situace, ale neříká nám nic o jednotlivých datech a proto se díváme do poslední, čtvrté tabulky
- Tabulka COEFFICIENTS
- B/Constant = intercept, aneb místo, v němž regresní přímka protíná osu Y, interpretujeme jako množství prodeje nahrávky v okamžiku, kdy investice do reklamy je nulová
- B/Nezávisle proměnná = sklon regresní přímky, získané číslo vyjadřuje, o kolik více nahrávek bude prodáno, navýšíme-li investici do reklamy o „1 jednotku“
- t + Sig = p hodnota a její vliv na zamítnutí / přijetí H0
- Na základě čísel získaných v této tabulce mohu předvídat prodej nahrávek dle objemu investovaných peněz do reklamy podle této „rovnice“
- Prodej nahrávky = „intercept“ + (sklon x finanční investice do reklamy)
Zdroje
Reference
- ↑ Hendl, J. (2009). Přehled statistických metod: Analýza a metaanalýza dat. Praha: Portál
- ↑ Hendl, J. (2006). Přehled statistických metod zpracování dat. Praha: Portál.
- ↑ Zvára, K. (2008). Regresní analýza. Praha: Matfypress.
- ↑ Regresní analýza. Retrieved from: http://cs.wikipedia.org/wiki/Regresní_analýza
- ↑ Field, A. (2007). Discovering Statistics Using IBM SPSS Statistics. Londýn: SAGE.
