Teorie sítí a nová média: Porovnání verzí

 
(Není zobrazeno 7 mezilehlých verzí od 4 dalších uživatelů.)
Řádek 1: Řádek 1:
−
== Teorie sítí ==
 
  
−
'''Teorie sítí''' spočívá ve studiu grafů jakožto reprezentací symetrických nebo asymetrických vztahů mezi diskrétními objekty. Má využití v mnoha disciplínách napříč obory - počítačová věda, ekonomie, biologie, sociologie a další. Zkoumání sítí nám může pomoci lépe pochopit například přenos, způsob distribuce a cestu informace na World Wide Webu, metabolické dráhy, logistické procesy či předvídat epidemiologické hrozby v síti kontaktů. Teorie sítí je součástí [[teorie grafů]] a spadá pod [[Teorie systémů|teorii systémů]], kterou řeší teoretická [[Kybernetika a nová média|kybernetika]].
+
'''Teorie sítí''' spočívá ve studiu grafů jakožto reprezentací symetrických nebo asymetrických vztahů mezi diskrétními objekty. Má využití v mnoha disciplínách napříč obory - počítačová věda, ekonomie, biologie, sociologie a další. Zkoumání sítí nám může pomoci lépe pochopit například přenos, způsob distribuce a cestu informace na World Wide Webu, metabolické dráhy, logistické procesy či předvídat epidemiologické hrozby v síti kontaktů.<ref>BARABÁSI, Albert-László. V pavučině sítí. Vyd. 1. V Praze: Paseka, 2005, 274 s. Fénix (Paseka). ISBN 80-718-5751-3.</ref> Teorie sítí je součástí [[teorie grafů]] a spadá pod [[Teorie systémů|teorii systémů]], kterou řeší teoretická [[Kybernetika a nová média|kybernetika]].
  
 
Sítě obecně chápeme jako zobrazení vztahů a vazeb mezi prvky (nejen) v sociálním prostoru. V sítích rozlišujeme tzv. [[uzly]] a [[hrany]], které tvoří graf sítě.
 
Sítě obecně chápeme jako zobrazení vztahů a vazeb mezi prvky (nejen) v sociálním prostoru. V sítích rozlišujeme tzv. [[uzly]] a [[hrany]], které tvoří graf sítě.
Řádek 9: Řádek 8:
 
==== Sedm mostů města Královce ====
 
==== Sedm mostů města Královce ====
  
−
Matematickou hádanku, kterou vyřešil Leonard Euler v 18. století, považujeme za první problém vyřešený pomocí teorií sítí. Hádanka zněla, za je možné všechny mosty přejít takovým způsobem, aby člověk vstoupil na každý most pouze jednou. Euler jako první dokázal, že to není možné, graf totiž nelze přejít tzv. [[eulerovským tahem]].
+
Matematickou hádanku, kterou vyřešil Leonard Euler v 18. století, považujeme za první problém vyřešený pomocí teorií sítí. Hádanka zněla, zda je možné všechny mosty přejít takovým způsobem, aby člověk vstoupil na každý most pouze jednou. Euler jako první dokázal, že to není možné, graf totiž nelze přejít tzv. [[eulerovským tahem]].
  
 
[[File:konigsberg.jpg|400px]]
 
[[File:konigsberg.jpg|400px]]
Řádek 29: Řádek 28:
 
=== Reference & seznam použité literatury ===
 
=== Reference & seznam použité literatury ===
 
<references/>
 
<references/>
 +
 +
[[Kategorie: Informační studia a knihovnictví]]
 +
[[Kategorie:Nová média a digitální kultura]]
 +
[[Kategorie:Hesla k opravě UISK]]

Aktuální verze z 21. 10. 2018, 13:08

Teorie sítí spočívá ve studiu grafů jakožto reprezentací symetrických nebo asymetrických vztahů mezi diskrétními objekty. Má využití v mnoha disciplínách napříč obory - počítačová věda, ekonomie, biologie, sociologie a další. Zkoumání sítí nám může pomoci lépe pochopit například přenos, způsob distribuce a cestu informace na World Wide Webu, metabolické dráhy, logistické procesy či předvídat epidemiologické hrozby v síti kontaktů.[1] Teorie sítí je součástí teorie grafů a spadá pod teorii systémů, kterou řeší teoretická kybernetika.

Sítě obecně chápeme jako zobrazení vztahů a vazeb mezi prvky (nejen) v sociálním prostoru. V sítích rozlišujeme tzv. uzly a hrany, které tvoří graf sítě.

Významnou osobností v teorii sítí je Albert-László Barabási, maďarsko-americký fyzik, který téma sítí zpracovává ve své knize V pavučině sítí.[2]

Sedm mostů města Královce

Matematickou hádanku, kterou vyřešil Leonard Euler v 18. století, považujeme za první problém vyřešený pomocí teorií sítí. Hádanka zněla, zda je možné všechny mosty přejít takovým způsobem, aby člověk vstoupil na každý most pouze jednou. Euler jako první dokázal, že to není možné, graf totiž nelze přejít tzv. eulerovským tahem.

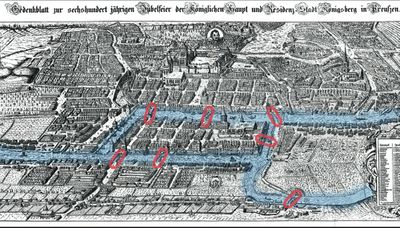
Konigsberg.jpg
zdroj obrázku: http://www.highiqpro.com/euler-puzzles

Šest stupňů odloučení

Též známé jako six degrees of separation je teorie, která říká, že se všichni lidé na planetě znají přes šest navzájem se propojených lidí. Teorie pochází z experimentu sociologa Stanleyho Milgrama, který v roce 1967 provedl pokus tzv. "malého světa".[3]

Teorie sítí a nová média

Vznik analýz sociálních sítí (tedy social network analysis, pro potřeby dalšího textu dále jen jako SNA) se datuje do 70. let minulého století. O něco později, v polovině 90. let, výzkum sítí řeší otázku aktérství. V počátečních pracích se výzkumníci zajímali jen o dva typy aktérů – ti byli buď lidští, nebo se jednalo o jejich skupinové abstrakce. Ke změně však došlo, když mezi „uzly“ sítí byly zahrnuty i koncepty, kategorie a narativy. Kromě "obyčejné" sociální sítě se začaly řešit tzv. silné a slabé vazby, konektivita uzlů a celkový kontext, který uzly a vazby propojuje. [4]

Související články

Reference & seznam použité literatury

  1. ↑ BARABÁSI, Albert-László. V pavučině sítí. Vyd. 1. V Praze: Paseka, 2005, 274 s. Fénix (Paseka). ISBN 80-718-5751-3.
  2. ↑ BARABÁSI, Albert-László. V pavučině sítí. Vyd. 1. V Praze: Paseka, 2005, 274 s. Fénix (Paseka). ISBN 80-718-5751-3.
  3. ↑ WATTS, Duncan J. Six degrees: the science of connected age. New York: W. W. Norton, c2003, 368 s. ISBN 03-930-4142-5.
  4. ↑ LACHMANN, Filip. Sophie Mützel: Sítě jako kulturně utvářené procesy [online]. [cit. 2015-09-19]. Dostupné z: http://socialniteorie.cz/sophie-mutzel-site-jako-kulturne-utvarene-procesy/
Citováno z „https://wikisofia.cz/w/index.php?title=Teorie_sítí_a_nová_média&oldid=55963“