Motýlí efekt: Porovnání verzí

m
Řádek 8: Řádek 8:
 
== Teorie chaosu ==
 
== Teorie chaosu ==
  
−
Teorie chaosu je teorie o nelineárních dynamických systémech, vykazují určitý vnitřní řád, který je velmi citlivý na počáteční podmínky. I když všechny vstupní rovnice jsou stoprocentně determinovány, jejich vzájemným působením dochází k jevu, o kterém nejsme schopni předpovědět vývoj situace, protože i malá změna na počátku může způsobit velký rozdíl ke konci situace. Toto chování je sice chaotické, avšak není nahodilé.<ref>Bussolari, C. J., & Goodell, J. A. (2009). Chaos Theory as a Model for Life Transitions Counseling: Nonlinear Dynamics and Life's Changes. Journal Of Counseling & Development, 87(1), 98-107.</ref> Teorii chaosu (znovu)založil E. Lorenz, kdy ji demonstroval na svém objevu, který se nazývá Podivný atraktor. [[Soubor:podivny atraktor.jpg|náhled|vpravo|Lorenzův dynamický systém s podivným atraktorem]]
+
Teorie chaosu je teorie o nelineárních dynamických systémech, vykazují určitý vnitřní řád, který je velmi citlivý na počáteční podmínky. I když všechny vstupní rovnice jsou stoprocentně determinovány, jejich vzájemným působením dochází k jevu, o kterém nejsme schopni předpovědět vývoj situace, protože i malá změna na počátku může způsobit velký rozdíl ke konci situace. Toto chování je sice chaotické, avšak není nahodilé.<ref>Bussolari, C. J., & Goodell, J. A. (2009). Chaos Theory as a Model for Life Transitions Counseling: Nonlinear Dynamics and Life's Changes. Journal Of Counseling & Development, 87(1), 98-107.</ref> Teorii chaosu (znovu)založil E. Lorenz, kdy ji demonstroval na svém objevu, který se nazývá Podivný atraktor. [[Soubor:podivny atraktor.jpg|náhled|vpravo|Křivka grafu Lorenzova podivného atraktoru]]
 
=== Atraktor ===
 
=== Atraktor ===
 
Nejznámější je Lorenzův podivný atraktor. Atraktor znamená konečný stav systému. E. Lorenz vzal a popsal pomocí několika jednoduchých rovnic chování vodního kola, které má místo lopatek děravé nádoby, do kterých přitéká voda a pohybuje s kolem. Lorenz očekával, že se kolo bude točit jedním směrem, anebo cyklicky měnit svůj směr, případně, že se zastaví. Vodní kolo je však nestabilní a nečekaně mění svůj směr otáčení, který se nedá předpovídat.Tyto data zadal do počítače, který znázornil graf. <ref>Sixta, T. (2014). Itnetwork.cz. Retrieved from: http://www.itnetwork.cz/fraktaly-a-chaos-pojednani-o-chaosu-a-atraktorech</ref>Křivka ve grafu se nikdy neprotíná a je nekonečná. Existují také bodové a cyklické atraktory.
 
Nejznámější je Lorenzův podivný atraktor. Atraktor znamená konečný stav systému. E. Lorenz vzal a popsal pomocí několika jednoduchých rovnic chování vodního kola, které má místo lopatek děravé nádoby, do kterých přitéká voda a pohybuje s kolem. Lorenz očekával, že se kolo bude točit jedním směrem, anebo cyklicky měnit svůj směr, případně, že se zastaví. Vodní kolo je však nestabilní a nečekaně mění svůj směr otáčení, který se nedá předpovídat.Tyto data zadal do počítače, který znázornil graf. <ref>Sixta, T. (2014). Itnetwork.cz. Retrieved from: http://www.itnetwork.cz/fraktaly-a-chaos-pojednani-o-chaosu-a-atraktorech</ref>Křivka ve grafu se nikdy neprotíná a je nekonečná. Existují také bodové a cyklické atraktory.
Řádek 14: Řádek 14:
 
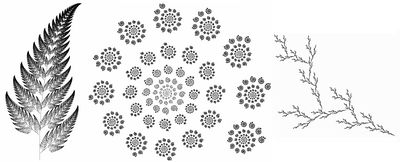
Fraktály je obrazec, ve kterém se opakuje podobný vzorec na různých úrovních. Když si fraktál rozdělíme a některé části zvětšíme, tak nalezneme podobnost mezi zmenšenou a velkou částí. Tento jev se nazývá soběpodobnost a je to charakteristická vlastnost pro chaotické systémy.<ref>http://en.wikipedia.org/wiki/Fractal</ref> Tato podobnost není nikdy stejná, ale je si velmi podobná. Znamená to, Tytu struktury jsou si velmi podobné avšak nejsou nikdy stejné.<ref>Vacík, P. (n.d.) Chaos: A co je za ním? (Excelentní studentská práce). VŠE. Retrieved from: http://nb.vse.cz/kfil/elogos/student/vaculik2.htm</ref>
 
Fraktály je obrazec, ve kterém se opakuje podobný vzorec na různých úrovních. Když si fraktál rozdělíme a některé části zvětšíme, tak nalezneme podobnost mezi zmenšenou a velkou částí. Tento jev se nazývá soběpodobnost a je to charakteristická vlastnost pro chaotické systémy.<ref>http://en.wikipedia.org/wiki/Fractal</ref> Tato podobnost není nikdy stejná, ale je si velmi podobná. Znamená to, Tytu struktury jsou si velmi podobné avšak nejsou nikdy stejné.<ref>Vacík, P. (n.d.) Chaos: A co je za ním? (Excelentní studentská práce). VŠE. Retrieved from: http://nb.vse.cz/kfil/elogos/student/vaculik2.htm</ref>
  
 +
:
 +
::::::[[File:fraktaly.jpg|400px]]
  
−
[[File:fraktaly.jpg|400px]]
+
:::::::::Ukázka fraktálů
−
Ukázka fraktálů
+
== Odkazy ==
  
−
== Reference ==
+
=== Reference ===
 
  <references/>.
 
  <references/>.
 +
=== Literatura===
 +
* Gleick, J. (1996). Chaos: vznik nové vědy. (349 s., Překlad Jaroslav Sedlář, Renata Kamenická). Brno: Ando Publishing.
 +
=== Odkazy na obrázky ===
 +
# Seanmcarney http://www.seanmcarney.com/blog/2014/1/19/the-butterfly-effect
 +
# Elektrorevue http://www.elektrorevue.cz/clanky/03019/kap_1.htm
 +
# Elektrorevue http://www.elektrorevue.cz/clanky/03019/kap_1.htm
 +
=== Klíčová slova ===

Verze z 1. 12. 2014, 19:05

Schéma motýlího efektu

Motýlí efekt (též známý jako efekt motýlích křídel) je jev, kdy malé změny ve vstupních podmínkách tohoto jevu mohou způsobit velké rozdíly v konečném důsledku. Efekt bývá připodobňován k mávnutí křídel motýla, který tímto činem způsobí hurikán tisíce kilometrů od něj. Tento pojem poprvé použil meteorolog Edward Lorenz 29. Prosince 1979. Je to ústřední charakteristika pro teorii chaosu.[1]



Teorie chaosu

Teorie chaosu je teorie o nelineárních dynamických systémech, vykazují určitý vnitřní řád, který je velmi citlivý na počáteční podmínky. I když všechny vstupní rovnice jsou stoprocentně determinovány, jejich vzájemným působením dochází k jevu, o kterém nejsme schopni předpovědět vývoj situace, protože i malá změna na počátku může způsobit velký rozdíl ke konci situace. Toto chování je sice chaotické, avšak není nahodilé.[2] Teorii chaosu (znovu)založil E. Lorenz, kdy ji demonstroval na svém objevu, který se nazývá Podivný atraktor.

Křivka grafu Lorenzova podivného atraktoru

Atraktor

Nejznámější je Lorenzův podivný atraktor. Atraktor znamená konečný stav systému. E. Lorenz vzal a popsal pomocí několika jednoduchých rovnic chování vodního kola, které má místo lopatek děravé nádoby, do kterých přitéká voda a pohybuje s kolem. Lorenz očekával, že se kolo bude točit jedním směrem, anebo cyklicky měnit svůj směr, případně, že se zastaví. Vodní kolo je však nestabilní a nečekaně mění svůj směr otáčení, který se nedá předpovídat.Tyto data zadal do počítače, který znázornil graf. [3]Křivka ve grafu se nikdy neprotíná a je nekonečná. Existují také bodové a cyklické atraktory.

Fraktály

Fraktály je obrazec, ve kterém se opakuje podobný vzorec na různých úrovních. Když si fraktál rozdělíme a některé části zvětšíme, tak nalezneme podobnost mezi zmenšenou a velkou částí. Tento jev se nazývá soběpodobnost a je to charakteristická vlastnost pro chaotické systémy.[4] Tato podobnost není nikdy stejná, ale je si velmi podobná. Znamená to, Tytu struktury jsou si velmi podobné avšak nejsou nikdy stejné.[5]

Fraktaly.jpg
Ukázka fraktálů

Odkazy

Reference

  1. ↑ Ozdemir, O., Ozdemir, P. G., & Yilmaz, E. (2014). The Butterfly Effect in Psychiatry: A case example. Journal Of Mood Disorders, 4(1), 34-37. doi:10.5455/jmood.20131205063836
  2. ↑ Bussolari, C. J., & Goodell, J. A. (2009). Chaos Theory as a Model for Life Transitions Counseling: Nonlinear Dynamics and Life's Changes. Journal Of Counseling & Development, 87(1), 98-107.
  3. ↑ Sixta, T. (2014). Itnetwork.cz. Retrieved from: http://www.itnetwork.cz/fraktaly-a-chaos-pojednani-o-chaosu-a-atraktorech
  4. ↑ http://en.wikipedia.org/wiki/Fractal
  5. ↑ Vacík, P. (n.d.) Chaos: A co je za ním? (Excelentní studentská práce). VŠE. Retrieved from: http://nb.vse.cz/kfil/elogos/student/vaculik2.htm

.

Literatura

  • Gleick, J. (1996). Chaos: vznik nové vědy. (349 s., Překlad Jaroslav Sedlář, Renata Kamenická). Brno: Ando Publishing.

Odkazy na obrázky

  1. Seanmcarney http://www.seanmcarney.com/blog/2014/1/19/the-butterfly-effect
  2. Elektrorevue http://www.elektrorevue.cz/clanky/03019/kap_1.htm
  3. Elektrorevue http://www.elektrorevue.cz/clanky/03019/kap_1.htm

Klíčová slova

Citováno z „https://wikisofia.cz/w/index.php?title=Motýlí_efekt&oldid=11080“