Huffmanovo kódování: Porovnání verzí

Řádek 1: Řádek 1:
 
= Základný popis =
 
= Základný popis =
−
Huffmanové kódovanie. Znaky, vyskytujúce sa vo vstupnom súbore najčastejšie, sa konvertujú  na bitové reťazce s najkratšou dĺžkou. Huffmanove kódovanie má vlastnosť prefixu, t.j. je jednoznačne dekódovateľné. Konštrukcia Huffmanovho kódovania je nejednoznačná t.j. výstupom môže byť viac kódov a jednotlivé kódové slová  nemusia mať rovnakú dľžku. Tento jav nastáva vtedy, keď pri redukcii najmenších pravdepodobností máme na výber z viacerých hodnôt. Aj napriek tomuto javu majú Huffmanove kódy sú najkratšie a majú rovnakú priemernú dĺžku.<ref>KRAVECOVÁ, Daniela. <i>Základy kódovania</i>. Košice: Technická univerzita v Košiciach, 2012. ISBN 978-80-553-1178-4. Dostupné také z: http://web.tuke.sk/fei-km/sites/default/files/prilohy/15/Zaklady_kodovania_ucebnica.pdf</ref>  
+
Znaky, vyskytujúce sa vo vstupnom súbore najčastejšie, sa konvertujú  na bitové reťazce s najkratšou dĺžkou. Huffmanove kódovanie má vlastnosť prefixu, t.j. je jednoznačne dekódovateľné. Konštrukcia Huffmanovho kódovania je nejednoznačná t.j. výstupom môže byť viac kódov a jednotlivé kódové slová  nemusia mať rovnakú dľžku. Tento jav nastáva vtedy, keď pri redukcii najmenších pravdepodobností máme na výber z viacerých hodnôt. Aj napriek tomuto javu majú Huffmanove kódy sú najkratšie a majú rovnakú priemernú dĺžku.<ref name=TUKE>KRAVECOVÁ, Daniela. <i>Základy kódovania</i>. Košice: Technická univerzita v Košiciach, 2012. ISBN 978-80-553-1178-4. Dostupné také z: http://web.tuke.sk/fei-km/sites/default/files/prilohy/15/Zaklady_kodovania_ucebnica.pdf</ref>  
 
= História=
 
= História=
 
David A. Huffman vynašiel algoritmus optimálneho kódovania v roku 1951, ešte počas štúdia na MIT, kde mu bola pridelená semestrálna práca na tému – najefektívnejší binárny kód. Túto prácu mu zadal jeho profesor Robert M. Fano. Huffman prišiel s ideou frekvenčného binárneho stromu a dokázal, že jeho metóda je najefektívnejšia.  Týmto predčil svojho profesora a odstránil hlavnú trhlinu – stavia strom z dola nahor namiesto zhora nadol.<ref><i>Huffman coding</i>. San Francisco: Wikimedia Foundation. Dostupné také z: https://en.wikipedia.org/wiki/Huffman_coding</ref>
 
David A. Huffman vynašiel algoritmus optimálneho kódovania v roku 1951, ešte počas štúdia na MIT, kde mu bola pridelená semestrálna práca na tému – najefektívnejší binárny kód. Túto prácu mu zadal jeho profesor Robert M. Fano. Huffman prišiel s ideou frekvenčného binárneho stromu a dokázal, že jeho metóda je najefektívnejšia.  Týmto predčil svojho profesora a odstránil hlavnú trhlinu – stavia strom z dola nahor namiesto zhora nadol.<ref><i>Huffman coding</i>. San Francisco: Wikimedia Foundation. Dostupné také z: https://en.wikipedia.org/wiki/Huffman_coding</ref>
 
= Konštrukcia kódu =
 
= Konštrukcia kódu =
−
* Usporiadame si pravdepodobnosti výskytu jednotlivých znakov zostupne
+
# Usporiadame si pravdepodobnosti výskytu jednotlivých znakov zostupne
−
* Sčítajú sa posledné dve pravdepodobnosti a výsledok zaradíme medzi ostatné pravdepodobnosti výskytu
+
# Sčítajú sa posledné dve pravdepodobnosti a výsledok zaradíme medzi ostatné pravdepodobnosti výskytu
−
*      Krok č. 2 opakujeme dovtedy, kým sa nedopracujeme k jednému znaku s pravdepodobnosťou 1
+
# Krok č. 2 opakujeme dovtedy, kým sa nedopracujeme k jednému znaku s pravdepodobnosťou 1
−
*      Výsledné kódové slová zapíšeme v opačnom poradí
+
# Výsledné kódové slová zapíšeme v opačnom poradí <ref name="TUKE" />
−
+
 
 +
== Príklad ==
 +
Na jednoduchom príklade si ukážeme konštrukciu Huffmanovho kódovania. Budeme postupovať podľa krokov uvedených vyššie.
 +
{| class="wikitable"
 +
|-
 +
! x<sub>i</sub> !! x1 !! x2 !! x3 !! x4 !! x5 !! x6 !! x7
 +
|-
 +
! P<sub>i</sub> !! 0,12 || 0,2 || 0,11 || 0,2 || 0,09 || 0,09 || 0,19
 +
|}
 +
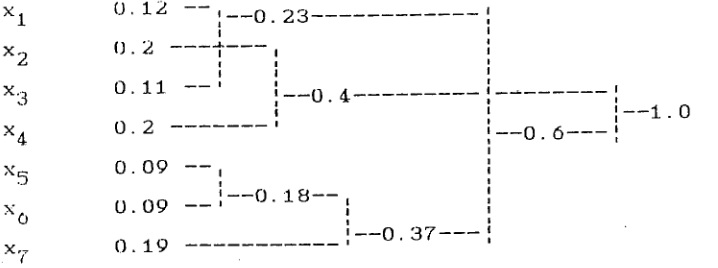
[[Soubor:Huffman1.jpg|střed|Konštrukcia stromu]] <ref>IVÁNEK, Jiří. <i>Vybrané kapitoly z matematické informatiky a znalostního inženýrství</i>. Praha: Státní nakladatelství technické literatury, 1990. ISBN 8070792175. Dostupné také z: http://uisk.xf.cz/podklady/ivanek3.pdf</ref>
 +
Ako máme možnosť vidieť na obrázku, postupne sa sčítavajú znaky s najnižšími pravdepodobnosťami, až kým sa nedporacujeme k pravdepodobnosti 1. Súčasne sa nám vytvoril strom, z ktorého vieme odčítať jednotlivé kódové slová. Na jednotlivé uzly si priradíme kódy 0 a 1.
 +
==== Výsledné kódy jednotlivých znakov ====
 +
{| class="wikitable"
 +
|-
 +
! x<sub>i</sub> !! x1 !! x2 !! x3 !! x4 !! x5 !! x6 !! x7
 +
|-
 +
! P<sub>i</sub> !! 100 || 00 || 101 || 01 || 1100 || 1101 || 111
 +
|}
 +
 
 +
=Odkazy=
 +
==Reference==
 
<references />
 
<references />

Verze z 15. 9. 2015, 10:25

Základný popis

Znaky, vyskytujúce sa vo vstupnom súbore najčastejšie, sa konvertujú na bitové reťazce s najkratšou dĺžkou. Huffmanove kódovanie má vlastnosť prefixu, t.j. je jednoznačne dekódovateľné. Konštrukcia Huffmanovho kódovania je nejednoznačná t.j. výstupom môže byť viac kódov a jednotlivé kódové slová nemusia mať rovnakú dľžku. Tento jav nastáva vtedy, keď pri redukcii najmenších pravdepodobností máme na výber z viacerých hodnôt. Aj napriek tomuto javu majú Huffmanove kódy sú najkratšie a majú rovnakú priemernú dĺžku.[1]

História

David A. Huffman vynašiel algoritmus optimálneho kódovania v roku 1951, ešte počas štúdia na MIT, kde mu bola pridelená semestrálna práca na tému – najefektívnejší binárny kód. Túto prácu mu zadal jeho profesor Robert M. Fano. Huffman prišiel s ideou frekvenčného binárneho stromu a dokázal, že jeho metóda je najefektívnejšia. Týmto predčil svojho profesora a odstránil hlavnú trhlinu – stavia strom z dola nahor namiesto zhora nadol.[2]

Konštrukcia kódu

  1. Usporiadame si pravdepodobnosti výskytu jednotlivých znakov zostupne
  2. Sčítajú sa posledné dve pravdepodobnosti a výsledok zaradíme medzi ostatné pravdepodobnosti výskytu
  3. Krok č. 2 opakujeme dovtedy, kým sa nedopracujeme k jednému znaku s pravdepodobnosťou 1
  4. Výsledné kódové slová zapíšeme v opačnom poradí [1]

Príklad

Na jednoduchom príklade si ukážeme konštrukciu Huffmanovho kódovania. Budeme postupovať podľa krokov uvedených vyššie.

xi x1 x2 x3 x4 x5 x6 x7
Pi 0,12 0,2 0,11 0,2 0,09 0,09 0,19
Konštrukcia stromu

[3]

Ako máme možnosť vidieť na obrázku, postupne sa sčítavajú znaky s najnižšími pravdepodobnosťami, až kým sa nedporacujeme k pravdepodobnosti 1. Súčasne sa nám vytvoril strom, z ktorého vieme odčítať jednotlivé kódové slová. Na jednotlivé uzly si priradíme kódy 0 a 1.

Výsledné kódy jednotlivých znakov

xi x1 x2 x3 x4 x5 x6 x7
Pi 100 00 101 01 1100 1101 111

Odkazy

Reference

  1. ↑ 1,0 1,1 KRAVECOVÁ, Daniela. Základy kódovania. Košice: Technická univerzita v Košiciach, 2012. ISBN 978-80-553-1178-4. Dostupné také z: http://web.tuke.sk/fei-km/sites/default/files/prilohy/15/Zaklady_kodovania_ucebnica.pdf
  2. ↑ Huffman coding. San Francisco: Wikimedia Foundation. Dostupné také z: https://en.wikipedia.org/wiki/Huffman_coding
  3. ↑ IVÁNEK, Jiří. Vybrané kapitoly z matematické informatiky a znalostního inženýrství. Praha: Státní nakladatelství technické literatury, 1990. ISBN 8070792175. Dostupné také z: http://uisk.xf.cz/podklady/ivanek3.pdf
Citováno z „https://wikisofia.cz/w/index.php?title=Huffmanovo_kódování&oldid=22615“