Náhodná veličina: Porovnání verzí
| Řádek 21: | Řádek 21: | ||
|} | |} | ||
<br /> | <br /> | ||
| − | Každé hodnotě xi je přiřazena právě jedna hodnota pi a pravděpodobnostní tabulku lze tedy chápat jako tabulkové určení funkce, kterou nazýváme ''pravděpodobnostní funkcí''<br /> | + | Každé hodnotě xi je přiřazena právě jedna hodnota pi a pravděpodobnostní tabulku lze tedy chápat jako tabulkové určení funkce, kterou nazýváme ''pravděpodobnostní funkcí''.<br /> |
| − | '''Definice pravděpodobnostní funkce:''' ''Pravděpodobnostní funkcí náhodné veličiny X nazýváme funkci p(x) = P(X = x)'' | + | '''Definice pravděpodobnostní funkce:''' ''Pravděpodobnostní funkcí náhodné veličiny X nazýváme funkci p(x) = P(X = x).'' |
| + | |||
== Zdroje == | == Zdroje == | ||
[[Kategorie: Statistika|*]] | [[Kategorie: Statistika|*]] | ||
Verze z 17. 4. 2014, 12:52
Náhodná veličina
Výsledky některých pokusů (elementární jevy) jsou přímo vyjádřeny číselně (padne 1), u jiných tomu tak není (padne líc). Také u těchto pokusů je účelné přiřadit elementárním jevům čísla.
Čísla přiřazená elementárním jevům tvoří obor hodnot M proměnné, kterou nazýváme náhodná veličina (označujeme X, Y, Z,...)
Definice náhodné veličiny
Náhodná veličina X je reálná funkce definovaná na množině všech elementárních jevů, která každému jevu přiřadí reálné číslo.
Např.: Hod mincí:
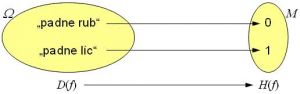
Podle oboru hodnot M rozdělujeme náhodné veličiny na:
- diskrétní: obor hodnot M je konečná nebo nekonečná posloupnost
- spojité: obor hodnot M je otevřený nebo uzavřený interval
Diskrétní náhodná veličina
Pravděpodobnostní funkce:
- Nechť X je diskrétní náhodná veličina s oborem možných hodnot {x1, x2, ..., en}, která tyto hodnoty nabývá s pravděpodobností {p1, p2, ..., pn}.
- Údaje sestavíme do tabulky:
| xi | x1 | x2 | xn |
| pi | p1 | p2 | pn |
Každé hodnotě xi je přiřazena právě jedna hodnota pi a pravděpodobnostní tabulku lze tedy chápat jako tabulkové určení funkce, kterou nazýváme pravděpodobnostní funkcí.
Definice pravděpodobnostní funkce: Pravděpodobnostní funkcí náhodné veličiny X nazýváme funkci p(x) = P(X = x).