Motýlí efekt: Porovnání verzí
m |
|||
| (Nejsou zobrazeny 2 mezilehlé verze od 2 dalších uživatelů.) | |||
| Řádek 2: | Řádek 2: | ||
'''Motýlí efekt '''(též známý jako efekt motýlích křídel) je jev, kdy malé změny ve vstupních podmínkách tohoto jevu mohou způsobit velké rozdíly v konečném důsledku. Efekt bývá připodobňován k mávnutí křídel motýla, který tímto činem způsobí hurikán tisíce kilometrů od něj. Tento pojem poprvé použil meteorolog Edward Lorenz 29. Prosince 1979. Je to ústřední charakteristika pro teorii chaosu.<ref name="1odkaz ">Ozdemir, O., Ozdemir, P. G., & Yilmaz, E. (2014). The Butterfly Effect in Psychiatry: A case example. Journal Of Mood Disorders, 4(1), 34-37. doi:10.5455/jmood.20131205063836</ref> | '''Motýlí efekt '''(též známý jako efekt motýlích křídel) je jev, kdy malé změny ve vstupních podmínkách tohoto jevu mohou způsobit velké rozdíly v konečném důsledku. Efekt bývá připodobňován k mávnutí křídel motýla, který tímto činem způsobí hurikán tisíce kilometrů od něj. Tento pojem poprvé použil meteorolog Edward Lorenz 29. Prosince 1979. Je to ústřední charakteristika pro teorii chaosu.<ref name="1odkaz ">Ozdemir, O., Ozdemir, P. G., & Yilmaz, E. (2014). The Butterfly Effect in Psychiatry: A case example. Journal Of Mood Disorders, 4(1), 34-37. doi:10.5455/jmood.20131205063836</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Teorie chaosu == | == Teorie chaosu == | ||
| − | |||
Teorie chaosu je teorie o nelineárních dynamických systémech, vykazují určitý vnitřní řád, který je velmi citlivý na počáteční podmínky. I když všechny vstupní rovnice jsou stoprocentně determinovány, jejich vzájemným působením dochází k jevu, o kterém nejsme schopni předpovědět vývoj situace, protože i malá změna na počátku může způsobit velký rozdíl ke konci situace. Toto chování je sice chaotické, avšak není nahodilé. Teorii chaosu (znovu)založil E. Lorenz, kdy ji demonstroval na svém objevu, který se nazývá Podivný atraktor.<ref name="1odkaz" /> <ref name="2odkaz ">Bussolari, C. J., & Goodell, J. A. (2009). Chaos Theory as a Model for Life Transitions Counseling: Nonlinear Dynamics and Life's Changes. Journal Of Counseling & Development, 87(1), 98-107.</ref> [[Soubor:podivny atraktor.jpg|náhled|vpravo|Křivka grafu Lorenzova podivného atraktoru]] | Teorie chaosu je teorie o nelineárních dynamických systémech, vykazují určitý vnitřní řád, který je velmi citlivý na počáteční podmínky. I když všechny vstupní rovnice jsou stoprocentně determinovány, jejich vzájemným působením dochází k jevu, o kterém nejsme schopni předpovědět vývoj situace, protože i malá změna na počátku může způsobit velký rozdíl ke konci situace. Toto chování je sice chaotické, avšak není nahodilé. Teorii chaosu (znovu)založil E. Lorenz, kdy ji demonstroval na svém objevu, který se nazývá Podivný atraktor.<ref name="1odkaz" /> <ref name="2odkaz ">Bussolari, C. J., & Goodell, J. A. (2009). Chaos Theory as a Model for Life Transitions Counseling: Nonlinear Dynamics and Life's Changes. Journal Of Counseling & Development, 87(1), 98-107.</ref> [[Soubor:podivny atraktor.jpg|náhled|vpravo|Křivka grafu Lorenzova podivného atraktoru]] | ||
=== Atraktor === | === Atraktor === | ||
Nejznámější je Lorenzův podivný atraktor. Atraktor znamená konečný stav systému. E. Lorenz vzal a popsal pomocí několika jednoduchých rovnic chování vodního kola, které má místo lopatek děravé nádoby, do kterých přitéká voda a pohybuje s kolem. Lorenz očekával, že se kolo bude točit jedním směrem, anebo cyklicky měnit svůj směr, případně, že se zastaví. Vodní kolo je však nestabilní a nečekaně mění svůj směr otáčení, který se nedá předpovídat.Tyto data zadal do počítače, který znázornil graf. Křivka ve grafu se nikdy neprotíná a je nekonečná. Existují také bodové a cyklické atraktory.<ref name="2odkaz" /> <ref>Sixta, T. (2014). Itnetwork.cz. Retrieved from: http://www.itnetwork.cz/fraktaly-a-chaos-pojednani-o-chaosu-a-atraktorech</ref> | Nejznámější je Lorenzův podivný atraktor. Atraktor znamená konečný stav systému. E. Lorenz vzal a popsal pomocí několika jednoduchých rovnic chování vodního kola, které má místo lopatek děravé nádoby, do kterých přitéká voda a pohybuje s kolem. Lorenz očekával, že se kolo bude točit jedním směrem, anebo cyklicky měnit svůj směr, případně, že se zastaví. Vodní kolo je však nestabilní a nečekaně mění svůj směr otáčení, který se nedá předpovídat.Tyto data zadal do počítače, který znázornil graf. Křivka ve grafu se nikdy neprotíná a je nekonečná. Existují také bodové a cyklické atraktory.<ref name="2odkaz" /> <ref>Sixta, T. (2014). Itnetwork.cz. Retrieved from: http://www.itnetwork.cz/fraktaly-a-chaos-pojednani-o-chaosu-a-atraktorech</ref> | ||
=== Fraktály === | === Fraktály === | ||
| − | + | Fraktál je obrazec, ve kterém se opakuje podobný vzorec na různých úrovních. Když si fraktál rozdělíme a některé části zvětšíme, tak nalezneme podobnost mezi zmenšenou a velkou částí. Tento jev se nazývá soběpodobnost a je to charakteristická vlastnost pro chaotické systémy. Tato podobnost není nikdy stejná, ale je si velmi podobná. Znamená to, Tytu struktury jsou si velmi podobné avšak nejsou nikdy stejné.<ref>http://en.wikipedia.org/wiki/Fractal</ref> <ref>Vacík, P. (n.d.) Chaos: A co je za ním? (Excelentní studentská práce). VŠE. Retrieved from: http://nb.vse.cz/kfil/elogos/student/vaculik2.htm</ref> | |
: | : | ||
| Řádek 18: | Řádek 13: | ||
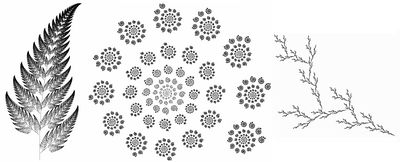
:::::::::Ukázka fraktálů | :::::::::Ukázka fraktálů | ||
| + | == Motýlí efekt v psychologii == | ||
| + | Efekt motýlích křídel můžeme připodobnit také k reálnému životu. Vždyť se nacházíme v jednom velkém chaotickém systému, ve kterém mohou způsobit i malé příčiny velké události. Toto lze aplikovat i v psychoterapii, kdy malá změna může způsobit velkou proměnu. Tento efekt může podpořit, ale i zhroutit efektivitu práce v psychoterapii. Co se stane, když v terapii projevíme drobnou nedůvěru, anebo ve správnou chvíli dáme drobnou radu? Může to ovlivnit výsledek spolupráce? | ||
| + | |||
| + | Nikdy nemůžeme zcela předpovědět důsledek myšlenky, proto bychom měli mít na paměti, že i malé drobnosti, mohou způsobit velké změny a teorie terapie je lineární, ale praxe je mnohem komplexnější.<ref>Moos, P.. (1999). Psychologie ve světle teorie chaosu. Scrigroup.com [online]. Retrieved from: http://www.scrigroup.com/limba/ceha-slovaca/46/Psychologie-ve-svtle-teorie-ch92465.php</ref> | ||
| + | |||
== Odkazy == | == Odkazy == | ||
| Řádek 30: | Řádek 30: | ||
=== Klíčová slova === | === Klíčová slova === | ||
teorie chaosu, fraktály, atraktor | teorie chaosu, fraktály, atraktor | ||
| + | [[Kategorie: Psychologie|*]] | ||
Aktuální verze z 9. 8. 2018, 14:48
Motýlí efekt (též známý jako efekt motýlích křídel) je jev, kdy malé změny ve vstupních podmínkách tohoto jevu mohou způsobit velké rozdíly v konečném důsledku. Efekt bývá připodobňován k mávnutí křídel motýla, který tímto činem způsobí hurikán tisíce kilometrů od něj. Tento pojem poprvé použil meteorolog Edward Lorenz 29. Prosince 1979. Je to ústřední charakteristika pro teorii chaosu.[1]
Obsah
Teorie chaosu
Teorie chaosu je teorie o nelineárních dynamických systémech, vykazují určitý vnitřní řád, který je velmi citlivý na počáteční podmínky. I když všechny vstupní rovnice jsou stoprocentně determinovány, jejich vzájemným působením dochází k jevu, o kterém nejsme schopni předpovědět vývoj situace, protože i malá změna na počátku může způsobit velký rozdíl ke konci situace. Toto chování je sice chaotické, avšak není nahodilé. Teorii chaosu (znovu)založil E. Lorenz, kdy ji demonstroval na svém objevu, který se nazývá Podivný atraktor.[1] [2]
Atraktor
Nejznámější je Lorenzův podivný atraktor. Atraktor znamená konečný stav systému. E. Lorenz vzal a popsal pomocí několika jednoduchých rovnic chování vodního kola, které má místo lopatek děravé nádoby, do kterých přitéká voda a pohybuje s kolem. Lorenz očekával, že se kolo bude točit jedním směrem, anebo cyklicky měnit svůj směr, případně, že se zastaví. Vodní kolo je však nestabilní a nečekaně mění svůj směr otáčení, který se nedá předpovídat.Tyto data zadal do počítače, který znázornil graf. Křivka ve grafu se nikdy neprotíná a je nekonečná. Existují také bodové a cyklické atraktory.[2] [3]
Fraktály
Fraktál je obrazec, ve kterém se opakuje podobný vzorec na různých úrovních. Když si fraktál rozdělíme a některé části zvětšíme, tak nalezneme podobnost mezi zmenšenou a velkou částí. Tento jev se nazývá soběpodobnost a je to charakteristická vlastnost pro chaotické systémy. Tato podobnost není nikdy stejná, ale je si velmi podobná. Znamená to, Tytu struktury jsou si velmi podobné avšak nejsou nikdy stejné.[4] [5]
- Ukázka fraktálů
Motýlí efekt v psychologii
Efekt motýlích křídel můžeme připodobnit také k reálnému životu. Vždyť se nacházíme v jednom velkém chaotickém systému, ve kterém mohou způsobit i malé příčiny velké události. Toto lze aplikovat i v psychoterapii, kdy malá změna může způsobit velkou proměnu. Tento efekt může podpořit, ale i zhroutit efektivitu práce v psychoterapii. Co se stane, když v terapii projevíme drobnou nedůvěru, anebo ve správnou chvíli dáme drobnou radu? Může to ovlivnit výsledek spolupráce?
Nikdy nemůžeme zcela předpovědět důsledek myšlenky, proto bychom měli mít na paměti, že i malé drobnosti, mohou způsobit velké změny a teorie terapie je lineární, ale praxe je mnohem komplexnější.[6]
Odkazy
Reference
- ↑ 1,0 1,1 Ozdemir, O., Ozdemir, P. G., & Yilmaz, E. (2014). The Butterfly Effect in Psychiatry: A case example. Journal Of Mood Disorders, 4(1), 34-37. doi:10.5455/jmood.20131205063836
- ↑ 2,0 2,1 Bussolari, C. J., & Goodell, J. A. (2009). Chaos Theory as a Model for Life Transitions Counseling: Nonlinear Dynamics and Life's Changes. Journal Of Counseling & Development, 87(1), 98-107.
- ↑ Sixta, T. (2014). Itnetwork.cz. Retrieved from: http://www.itnetwork.cz/fraktaly-a-chaos-pojednani-o-chaosu-a-atraktorech
- ↑ http://en.wikipedia.org/wiki/Fractal
- ↑ Vacík, P. (n.d.) Chaos: A co je za ním? (Excelentní studentská práce). VŠE. Retrieved from: http://nb.vse.cz/kfil/elogos/student/vaculik2.htm
- ↑ Moos, P.. (1999). Psychologie ve světle teorie chaosu. Scrigroup.com [online]. Retrieved from: http://www.scrigroup.com/limba/ceha-slovaca/46/Psychologie-ve-svtle-teorie-ch92465.php
.
Doporučená literatura
- Gleick, J. (1996). Chaos: vznik nové vědy. (349 s., Překlad Jaroslav Sedlář, Renata Kamenická). Brno: Ando Publishing.
Odkazy na obrázky
- Seanmcarney http://www.seanmcarney.com/blog/2014/1/19/the-butterfly-effect
- Elektrorevue http://www.elektrorevue.cz/clanky/03019/kap_1.htm
- Elektrorevue http://www.elektrorevue.cz/clanky/03019/kap_1.htm
Klíčová slova
teorie chaosu, fraktály, atraktor