Shannon-Fanovo kódování: Porovnání verzí
| Řádek 3: | Řádek 3: | ||
* Řešení nemusí být vždy optimální (nejkratší) | * Řešení nemusí být vždy optimální (nejkratší) | ||
| − | * Používá se v kompresních datech [https://files.klaska.net/sites/files.klaska.net/files/manual_files/cvut/Teorie%20kodovani/Shannon-Fanovo%20k_dov_n_.pdf] | + | * Používá se v kompresních datech [https://files.klaska.net/sites/files.klaska.net/files/manual_files/cvut/Teorie%20kodovani/Shannon-Fanovo%20k_dov_n_.pdf] |
| − | + | * Asymetrická kompresní metoda | |
| + | * Dvouprůchodová kompresní metoda | ||
| + | * Semi-adaptivní kompresní metoda | ||
| + | * Dosahuje horších výsledků ve srovnání s Huffmanovým kódováním[http://www.stringology.org/DataCompression/sf/index_cs.html] | ||
| + | C.E.Shannon [[File:shannon.jpg|120px|C.E.Shannon]] [https://history-computer.com/ModernComputer/thinkers/Shannon.html] | ||
==Konstrukce binárního kódu== | ==Konstrukce binárního kódu== | ||
Verze z 19. 12. 2018, 09:44
Základní popis
Shannon-Fanovo kódování je technika pro sestavení prefixového kódu založená na seznamu symbolů a počtech jejich výskytů. v roce 1949 metodu nezávisle na sobě publikovali Claude Elwood Shannon (otec teorie informace)[1] s Warrenem Weaverem a Robertem Mario Fano.[2]
- Řešení nemusí být vždy optimální (nejkratší)
- Používá se v kompresních datech [3]
- Asymetrická kompresní metoda
- Dvouprůchodová kompresní metoda
- Semi-adaptivní kompresní metoda
- Dosahuje horších výsledků ve srovnání s Huffmanovým kódováním[4]
C.E.Shannon[5]
Konstrukce binárního kódu
Princip
Princip je založen na množině znaků rekursivně dělících se vždy na dvě podmnožiny, aby součet výskytů znaků v obou podmnožinách byl přibližně stejný. Jedné podmnožině je pak v kódu přiřazena binární 1 a druhé 0.[6]
- Postup není optimální
- Důležitá vlastnost: opětovné prefixovost
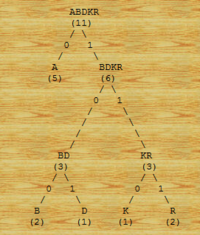
Prefixovost Shannon-Fanova kódu můžeme zachytit binárním prefixovým stromem. Písmena vstupní abecedy jsou v listech a jejich kódy tvoří od cesta od kořene do daného vrcholu.
- Neprefixový kód = na cestě do nějakého listu leží nějaké písmeno vstupní abecedy[7]
Příklad
- Vstupní soubor: ABRAKADABRA
- Jednotlivé znaky: A B D K R
- Počty výskytů: (5) (2) (1) (1) (2)
- Vytvořený strom: