Konstrukce rozhodovacích stromů (princip snižování entropie): Porovnání verzí

(Založena nová stránka s textem „= Rozhodovací stromy = Nejčastěji se koncept rozhodovacích stromů používá v oblasti výpočetní techniky. Tato metoda spadá mezi metody dobýván…“)
 
 
(Není zobrazeno 14 mezilehlých verzí od stejného uživatele.)
Řádek 1: Řádek 1:
−
= Rozhodovací stromy =
+
== Rozhodovací stromy ==
−
Nejčastěji se koncept rozhodovacích stromů používá v oblasti výpočetní techniky. Tato metoda spadá mezi metody dobývání znalostí, jejichž cílem je dojít informacím za pomoci předem získaných dat a nalézt v datech vzájemné závislosti.< ref>[https://dspace.cuni.cz/bitstream/handle/20.500.11956/30665/DPTX_0_0_11320_0_213500_0_43071.pdf?sequence=1&isAllowed=y]JAHODA, Miroslav. Rozhodovací stromy. Praha, 2009. Diplomová práce. Univerzita Karlova. Vedoucí práce Doc. RNDr. Iveta Mrázová, CSc.</ref>
+
Jedná se o princip rozhodování o něčem. Používají se buďto rozhodovací tabulky a nebo ke grafickému znázornění právě rozhodovací stromy. Nejčastěji se koncept rozhodovacích stromů používá v oblasti výpočetní techniky. Tato metoda spadá mezi metody dobývání znalostí, jejichž cílem je dojít k informacím za pomoci předem získaných dat a nalézt v datech vzájemné závislosti.<ref>[https://dspace.cuni.cz/bitstream/handle/20.500.11956/30665/DPTX_0_0_11320_0_213500_0_43071.pdf?sequence=1&isAllowed=y]JAHODA, Miroslav. Rozhodovací stromy. Praha, 2009. Diplomová práce. Univerzita Karlova. Vedoucí práce Doc. RNDr. Iveta Mrázová, CSc.</ref> Rozhodovací stromy vizuálně znázorňují celý proces rozhodování a cestu ke správnému výsledku. Všechny možnosti, dotazy a odpovědi jsou vidět zároveň.
  
 +
=== Struktura ===
 +
[[Soubor:Rozhodovaci stromy konstrukce.png|náhled|vpravo|popis konstrukce rozhodovacího stromu]]
 +
Základem (počátek dotazu) je ''výchozí uzel'', tzv. ''kořen stromu''. Obsahuje první otázku. Podle získané odpovědi pokračujeme po odpovídající hraně do příslušného podstromu a tak dál, až dojdeme ke konečné odpovědi. Ta je zapsaná v tzv. ''listu'', tedy uzlu, ze kterého nevedou další hrany (protože neklade další otázky). Počet úrovní stromu od kořene k nejzazšímu listu nazýváme výškou stromu.<ref>[https://popelka.ms.mff.cuni.cz/~lessner/mw/index.php/U%C4%8Debnice/Informace/Rozhodovac%C3%AD_stromy_a_chytr%C3%A9_ot%C3%A1zky]</ref>
  
 +
* '''Kořen stromu''', je uzel do nějž nevstupují žádné hrany, do
 +
ostatních uzlů vstupuje právě jedna hrana.
 +
* '''Terminální uzly (listy stromu)''' jsou ty vrcholy, z nichž žádná hrana
 +
nevystupuje.
 +
* '''Neterminálním (rozhodovacím) uzlům''' jsou přiřazeny otázky Q1,...,Qn tak, že na
 +
žádné cestě z kořene se nesmí žádná otázka opakovat.
 +
* z každého neterminálního uzlu vycházejí '''orientované (přechodové) hrany (větve)'''
 +
označené jednotlivými možnými odpověďmi na přiřazenou otázku. znázorňují tedy všechny možné alternativy.
 +
* terminálním uzlům jsou přiřazena '''rozhodnutí'''.<ref>[https://sites.ff.cuni.cz/uisk/wp-content/uploads/sites/62/2016/01/Stru%c4%8dn%c4%9b-o-rozhodovac%c3%adch-tabulk%c3%a1ch-a-konstrukci-rozhodovac%c3%adch-strom%c5%af_Iv%c3%a1nek.pdf]</ref>
 +
<br/>
 +
Rozhodovací stromy mohou být konstruované i ze strany. Kořen nemusí být horním vrcholem. Princip zůstává stejný.
 +
[[Soubor:Rozhodovaci strom.png|bezrámu|střed|rozhodovací strom]]
  
 +
== Princip snižování entropie ==
 +
 +
=== Informace ===
 +
Pojem informace má mnoho definic, ovšem z pohledu rozhodování je nejpříhodnější ji definovat jako ''úbytek entropie''(neboli možností). Každá další informace v rozhodovacím stromě nás přiblíží ke správnému rozhodnutí tak, že ubyde naše nevědomost v rámci problematiky a tím i možnosti v rozhodování.
 +
 +
==== Informace a pravděpodobnost ====
 +
 +
=== Entropie ===
 +
''Entropie'', neboli chaos. Míra entropie vyjadřuje například míru nevědomosti, neuspořádanost systému, šum v přenosu dat či nedostatek informační hodnoty ve sdělení. Čím víc máme informací k danému tématu, otázce, problému, tím se snižuje míra entropie.
 +
 +
 +
=== Reference ===
 
<references />
 
<references />

Aktuální verze z 28. 12. 2021, 10:22

Rozhodovací stromy

Jedná se o princip rozhodování o něčem. Používají se buďto rozhodovací tabulky a nebo ke grafickému znázornění právě rozhodovací stromy. Nejčastěji se koncept rozhodovacích stromů používá v oblasti výpočetní techniky. Tato metoda spadá mezi metody dobývání znalostí, jejichž cílem je dojít k informacím za pomoci předem získaných dat a nalézt v datech vzájemné závislosti.[1] Rozhodovací stromy vizuálně znázorňují celý proces rozhodování a cestu ke správnému výsledku. Všechny možnosti, dotazy a odpovědi jsou vidět zároveň.

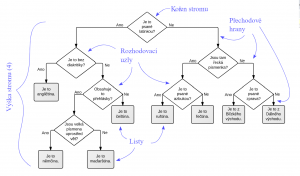
Struktura

popis konstrukce rozhodovacího stromu

Základem (počátek dotazu) je výchozí uzel, tzv. kořen stromu. Obsahuje první otázku. Podle získané odpovědi pokračujeme po odpovídající hraně do příslušného podstromu a tak dál, až dojdeme ke konečné odpovědi. Ta je zapsaná v tzv. listu, tedy uzlu, ze kterého nevedou další hrany (protože neklade další otázky). Počet úrovní stromu od kořene k nejzazšímu listu nazýváme výškou stromu.[2]

  • Kořen stromu, je uzel do nějž nevstupují žádné hrany, do

ostatních uzlů vstupuje právě jedna hrana.

  • Terminální uzly (listy stromu) jsou ty vrcholy, z nichž žádná hrana

nevystupuje.

  • Neterminálním (rozhodovacím) uzlům jsou přiřazeny otázky Q1,...,Qn tak, že na

žádné cestě z kořene se nesmí žádná otázka opakovat.

  • z každého neterminálního uzlu vycházejí orientované (přechodové) hrany (větve)

označené jednotlivými možnými odpověďmi na přiřazenou otázku. znázorňují tedy všechny možné alternativy.

  • terminálním uzlům jsou přiřazena rozhodnutí.[3]


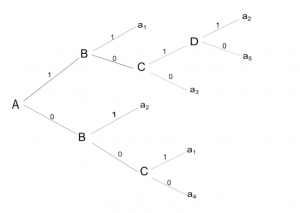
Rozhodovací stromy mohou být konstruované i ze strany. Kořen nemusí být horním vrcholem. Princip zůstává stejný.

rozhodovací strom

Princip snižování entropie

Informace

Pojem informace má mnoho definic, ovšem z pohledu rozhodování je nejpříhodnější ji definovat jako úbytek entropie(neboli možností). Každá další informace v rozhodovacím stromě nás přiblíží ke správnému rozhodnutí tak, že ubyde naše nevědomost v rámci problematiky a tím i možnosti v rozhodování.

Informace a pravděpodobnost

Entropie

Entropie, neboli chaos. Míra entropie vyjadřuje například míru nevědomosti, neuspořádanost systému, šum v přenosu dat či nedostatek informační hodnoty ve sdělení. Čím víc máme informací k danému tématu, otázce, problému, tím se snižuje míra entropie.


Reference

  1. ↑ [1]JAHODA, Miroslav. Rozhodovací stromy. Praha, 2009. Diplomová práce. Univerzita Karlova. Vedoucí práce Doc. RNDr. Iveta Mrázová, CSc.
  2. ↑ [2]
  3. ↑ [3]
Citováno z „https://wikisofia.cz/w/index.php?title=Konstrukce_rozhodovacích_stromů_(princip_snižování_entropie)&oldid=69048“