Principy statistické indukce: Porovnání verzí
m (Ondřej Novák (mellorian@inmail.cz) přesunul stránku Principy statistické indukce (základní soubor a výběr) na Principy statistické indukce: Nový název postačuje.) |
|||
| Řádek 1: | Řádek 1: | ||
| + | [[Soubor:Zakladni-soubor-vyberovy-soubor.jpg|vpravo|Principy statistické indukce|300px]] | ||
''V tomto článku jsou zmiňována následující témata'': deskriptivní statistika, induktivní statistika, základní soubor, populace, výběr, parametr, rozsah výběru, principy usuzování. | ''V tomto článku jsou zmiňována následující témata'': deskriptivní statistika, induktivní statistika, základní soubor, populace, výběr, parametr, rozsah výběru, principy usuzování. | ||
== Přístupy statistického zkoumání == | == Přístupy statistického zkoumání == | ||
Verze z 14. 5. 2014, 13:26
V tomto článku jsou zmiňována následující témata: deskriptivní statistika, induktivní statistika, základní soubor, populace, výběr, parametr, rozsah výběru, principy usuzování.
Obsah
Přístupy statistického zkoumání
Deskriptivní (popisná) statistika
- zabývá se úplným popisem, účelnou sumarizací a uspořádáním zvoleného souboru statistických jednotek;
- představuje organizaci dat a popis dat užitím grafů, numerických souhrnů a dalších matematicky propracovaných prostředků;
- obvykle předchází resp. doplňuje induktivní statistiku svým popisným charakterem (vymezením parametrů).
Induktivní statistika
- se namísto zkoumání celého základního souboru (populace), zabývá se zkoumáním zvoleného vzorku (výběru) v rámci celého základního souboru;
- je proces zobecňování úsudků o vlastnostech populace založený na informacích z náhodných vzorek = skrze metody induktivní statistiky se snažíme odvodit tvrzení platná pro celý základní soubor (populace).
- řeší dva typy úkolů: odhad parametrů a testování statistických hypotéz.
Cílem induktivní statistiky je z vypozorovaných dat vyvodit zobecnitelná tvrzení s udáním intervalu spolehlivosti - jde tedy o snahu objektivizovat pozorování a zbavit se subjektivního vlivu pozorovatele. Hladina intervalu spolehlivosti určuje, s jakou pravděpodobností pokryje výběrový průměr, průměr základního souboru při opakovaném testování.
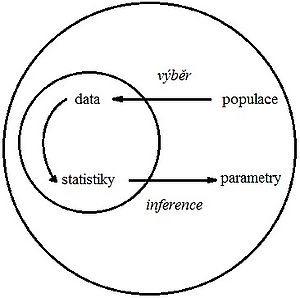
Populace a výběr
Základní soubor (populace)
Je množina všech teoreticky možných objektů (např. jedinců) v uvažované situaci = statistický soubor, který je vymezen cílem výzkumu a pro který vyvozujeme závěry výzkumného šetření.
- charakterizuje se parametrem, což je např. výška, váha, IQ, atp.
- má konečný nebo nekonečný (hypotetický) rozsah, který je dán N (např.: N = 150 lidí, opic, rostlin,...).
Výběrový soubor (výběr)
Je část populace vybrané na základě předem stanovených kritérii resp. pravidel (podmnožina základního souboru).
- O náhodném výběru uvažujeme, když splňuje dvě základní vlastnosti: pravděpodobnost zařazení do vzorku je pro všechny statistické jednotky populace nenulová a statistické jednotky jsou do vzorku vybrané nezávisle jedna od druhé.
- O reprezentativním výběru uvažujeme, když výběrový soubor dobře odráží strukturu celého zkoumaného souboru.
Principy statistického usuzování
- Statistické usuzování znamená zobecňování z výběrových statistik na parametry rozdělení.
- Abychom mohli provést statistické usuzování, musíme mít nějakou teorii, jež popisuje náhodné chování sledovaných proměnných.
- Existují dva typy výběrových chyb: náhodné výběrové chyby a systematické chyby. Získáním náhodného výběru zmenšujeme systematickou chybu a získáváme podklad pro odhad náhodné výběrové chyby.
- Výběrová rozdělení statistik jsou teoretická pravděpodobnostní rozdělení, která popisují vztah mezi výběrovou statistikou a populací.
- Směrodatná odchylka výběrového rozdělení statistiky (odhad parametru) se nazývá směrodatná chyba. Odhaduje náhodnou výběrovou chybu vypočítané statistiky (odhadu parametru).
- Jak roste velikost výběru, výběrová chyba a směrodatná chyba se zmenšují.
- Směrodatná chyba se používá k získání intervalového odhadu parametrů i k testování hypotéz o parametrech rozdělení.
Reference
- Hendl, J. (2004). Přehled statistických metod zpracování dat: analýza a metaanalýza dat. Praha: Portál.
- Zvára, K. (2006). Biostatistika. Praha: Karolinum.
- Zvárová, J. (2011). Biomedicínská statistika. Praha: Karolinum.