Shannon-Fanovo kódování: Porovnání verzí
| Řádek 1: | Řádek 1: | ||
=Základný popis= | =Základný popis= | ||
Je pomenované po Claude Elwood Shannonovi a Robertovi Fanovi, ktorí zostrojili kód s vlastnosťou prefixu na základe pravdepodobností výskytu znakov. | Je pomenované po Claude Elwood Shannonovi a Robertovi Fanovi, ktorí zostrojili kód s vlastnosťou prefixu na základe pravdepodobností výskytu znakov. | ||
| − | |||
| − | |||
=Konštrukcia kódu= | =Konštrukcia kódu= | ||
Postup konštrukcie je podobný ako pri Huffmanovom kódovaní. Rozdiel spočíva len smere konštrukcie binárneho stromu. | Postup konštrukcie je podobný ako pri Huffmanovom kódovaní. Rozdiel spočíva len smere konštrukcie binárneho stromu. | ||
| Řádek 30: | Řádek 28: | ||
=Využitie= | =Využitie= | ||
V praxi sa využíva omnoho menej než Huffmanove kódovanie, pretože nie vždy produkuje optimálny kód, ale aj napriek tomu sa využíva pri kompresii dát vo formáte ZIP. | V praxi sa využíva omnoho menej než Huffmanove kódovanie, pretože nie vždy produkuje optimálny kód, ale aj napriek tomu sa využíva pri kompresii dát vo formáte ZIP. | ||
| + | ==Odkazy== | ||
| + | ===Reference=== | ||
<references/> | <references/> | ||
| + | ==Súvisiace články== | ||
| + | [[Optimální (entropické) kódování informačního zdroje]] | ||
| + | [[Huffmanove kódovanie]] | ||
Verze z 16. 9. 2015, 02:26
Obsah
Základný popis
Je pomenované po Claude Elwood Shannonovi a Robertovi Fanovi, ktorí zostrojili kód s vlastnosťou prefixu na základe pravdepodobností výskytu znakov.
Konštrukcia kódu
Postup konštrukcie je podobný ako pri Huffmanovom kódovaní. Rozdiel spočíva len smere konštrukcie binárneho stromu.
- Jednotlivé znaky si zoradíme zostupne podľa pravdepodobnosti výskytu
- Pri zachovaní poradia znakov, rozdelíme množinu na dve časti tak, aby bol výsledný rozdiel súčtov pravdepodobnosti čo najmenší
- Jednotlivým častiam pridelíme kódový znak 0 alebo 1
- Kroky 2 a 3 opakujeme dovtedy, kým sa nedopracujeme k jednoprvkovým množinám
- Jednotlivé kódové slová získame čítaním kódových znakov v poradí v akom im boli prideľované [1]
Príklad
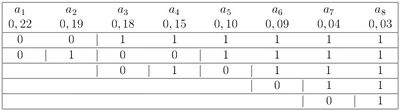
Konštrukciu stromu podľa vyššie uvedeného postupu si ukážeme na jednoduchom príklade:
| Zdrojová abeceda | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
|---|---|---|---|---|---|---|---|---|
| Pravdepodobnosť výskytu | 0,22 | 0,19 | 0,18 | 0,15 | 0,10 | 0,09 | 0,04 | 0,03 |
Jednotlivé kódové slová sa čítajú zhora nadol. V nasledujúcej tabuľke sú zobrazené výsledné kódové slová:
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
|---|---|---|---|---|---|---|---|
| 00 | 01 | 100 | 101 | 110 | 1110 | 11110 | 11111 |
Využitie
V praxi sa využíva omnoho menej než Huffmanove kódovanie, pretože nie vždy produkuje optimálny kód, ale aj napriek tomu sa využíva pri kompresii dát vo formáte ZIP.
Odkazy
Reference
- ↑ IVÁNEK, Jiří. Vybrané kapitoly z kódování informací. Praha, 2007. Dostupné také z: texty.jinonice.cuni.cz/studijni-texty/ivanek-jiri/ivanek_01.pdf/attachment_download/file
- ↑ KRAVECOVÁ, Daniela. Základy kódovania. Košice: Technická univerzita v Košiciach, 2012. ISBN 978-80-553-1178-4. Dostupné také z: http://web.tuke.sk/fei-km/sites/default/files/prilohy/15/Zaklady_kodovania_ucebnica.pdf
Súvisiace články
Optimální (entropické) kódování informačního zdroje Huffmanove kódovanie
Text je dostupný pod licencí Creative Commons Uveďte autora 3.0 Česko při dodržení případných autorských práv a dalších podmínek
© 2013 ISSN: 2336-5897
