Metody popisování polohy: Porovnání verzí
| Řádek 4: | Řádek 4: | ||
| − | Míry polohy slouží k popsání tzv. centrální tendence dané proměnné. Velmi často jde o první ukazatel, který nás zajímá, chceme-li si udělat představu o tom, jak data vypadají. Míry polohy nám dokáží odpovědět na otázky jako: "Jak byli zhruba účastníci studie staří?", nebo "Jaká byla nejčastější známka studentů psychologie ze statistiky?". Jaký statistický ukazatel máme zvolit nám často napoví [[Typy proměnných|typ proměnné]]. Ve specifických případech ovšem volíme ukazatel jiný (příklady jsou uvedeny u konkrétních ukazatelů). <ref name="Hendl"> | + | Míry polohy slouží k popsání tzv. centrální tendence dané proměnné. Velmi často jde o první ukazatel, který nás zajímá, chceme-li si udělat představu o tom, jak data vypadají. Míry polohy nám dokáží odpovědět na otázky jako: "Jak byli zhruba účastníci studie staří?", nebo "Jaká byla nejčastější známka studentů psychologie ze statistiky?". Jaký statistický ukazatel máme zvolit nám často napoví [[Typy proměnných|typ proměnné]]. Ve specifických případech ovšem volíme ukazatel jiný (příklady jsou uvedeny u konkrétních ukazatelů). <ref name="Hendl">Hendl, J.(2012). Přehled statistických metod: Analýza a metaanalýza dat. Praha: Portál <ref> |
=== Modus === | === Modus === | ||
| Řádek 38: | Řádek 38: | ||
Průměr se používá především na kvantitativní data, ovšem ve výjimečných případech se dá použít na proměnnou ordinální (např. školní známka). | Průměr se používá především na kvantitativní data, ovšem ve výjimečných případech se dá použít na proměnnou ordinální (např. školní známka). | ||
| − | '''Jednou z vlastností průměru''' je jeho senzitivita vůči odlehlým hodnotám. V souboru hodnot, kde se vyskytne nějaká extrémní hodnota, tak může zkreslovat. Typickým příkladem je např. průměrný plat. Hodně lidí je na tom většinou podobně , pár lidí se má o trochu lépe či hůře, a pak je tu mála skupina lidí, kteří vydělávají mnohonásobně víc, než ostatní. Těchto pár procent lidí může s průměrem platů zcela zásadně hnout, i když realita je pro většinu zbylých lidí jiná. Pro takový případ se často spokojíme s mediánem, který odlehlou hodnotou není tak zasažen. Další způsob může být tzv. ''trimmed mean'', kde zkrátka ignorujeme určité procento nejzazších hodnot na obou stranách. K dispozici je ovšem spousta dalších metod (spadajících pod takzvané robustní metody, protože odolávají určitým deviacím dat od našich očekávání), ty zde uvedeny nebudou. Pro zvídavého čtenáře ovšem doporučuji mohykána v oblasti robustních metod, Randa Wilcoxe. <ref name="Wilcox"> | + | '''Jednou z vlastností průměru''' je jeho senzitivita vůči odlehlým hodnotám. V souboru hodnot, kde se vyskytne nějaká extrémní hodnota, tak může zkreslovat. Typickým příkladem je např. průměrný plat. Hodně lidí je na tom většinou podobně , pár lidí se má o trochu lépe či hůře, a pak je tu mála skupina lidí, kteří vydělávají mnohonásobně víc, než ostatní. Těchto pár procent lidí může s průměrem platů zcela zásadně hnout, i když realita je pro většinu zbylých lidí jiná. Pro takový případ se často spokojíme s mediánem, který odlehlou hodnotou není tak zasažen. Další způsob může být tzv. ''trimmed mean'', kde zkrátka ignorujeme určité procento nejzazších hodnot na obou stranách. K dispozici je ovšem spousta dalších metod (spadajících pod takzvané robustní metody, protože odolávají určitým deviacím dat od našich očekávání), ty zde uvedeny nebudou. Pro zvídavého čtenáře ovšem doporučuji mohykána v oblasti robustních metod, Randa Wilcoxe. <ref name="Wilcox">Wilcox, R. (2012). Introduction to Robust Estimation and Hypothesis Testing (3rd ed.). Academic Press.</ref> |
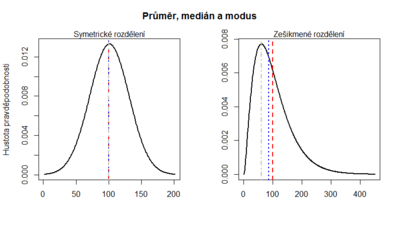
Obecně platí, že pokud je rozložení dat symetrické, pak <math>\bar{x}=\tilde{x}=\hat{x}</math>. Pokud se tyto ukazatele výrazně liší, může to být ukazatel toho, že je potřeba data prozkoumat víc zblízka. | Obecně platí, že pokud je rozložení dat symetrické, pak <math>\bar{x}=\tilde{x}=\hat{x}</math>. Pokud se tyto ukazatele výrazně liší, může to být ukazatel toho, že je potřeba data prozkoumat víc zblízka. | ||
Verze z 28. 11. 2016, 12:43
Popisování míry polohy
Upozornění: Tato stránka je poněkud školometská, protože pojednává o základních metodách, které prostě musíme umět a nejsou ničím zábavné. Pokud má laskavý čtenáŕ více času a zvídavosti, nechť se nechá přesměrovat na perfektní vida Khanovy školy, kde mu vše bude vysvětleno zábavněji, než zde :)
Míry polohy slouží k popsání tzv. centrální tendence dané proměnné. Velmi často jde o první ukazatel, který nás zajímá, chceme-li si udělat představu o tom, jak data vypadají. Míry polohy nám dokáží odpovědět na otázky jako: "Jak byli zhruba účastníci studie staří?", nebo "Jaká byla nejčastější známka studentů psychologie ze statistiky?". Jaký statistický ukazatel máme zvolit nám často napoví typ proměnné. Ve specifických případech ovšem volíme ukazatel jiný (příklady jsou uvedeny u konkrétních ukazatelů). Chybná citace: Chybí ukončovací </ref> k tagu <ref>
Obecně platí, že pokud je rozložení dat symetrické, pak . Pokud se tyto ukazatele výrazně liší, může to být ukazatel toho, že je potřeba data prozkoumat víc zblízka.
Dokážete říct, která z čar na grafu představuje modus, medián a průměr? Který z ukazatelů je v příkladech vhodný jako ukazatel centrální tendence?