Metody popisování polohy: Porovnání verzí
(→Zadání) |
|||
| Řádek 44: | Řádek 44: | ||
=Rozvíjení intuice= | =Rozvíjení intuice= | ||
==Zadání== | ==Zadání== | ||
| + | Nyní si ukážeme na několika příkladech jakým způsobem se míry polohy chovají. V této sekci si můžete vyzkoušet zodpovědět na otázky sami, v další sekci se můžete podívat na řešení. | ||
| + | |||
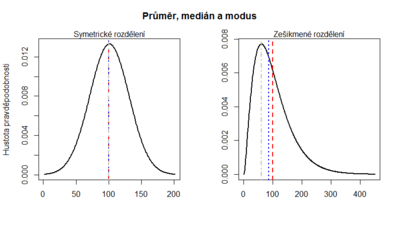
===Míry polohy a rozložení=== | ===Míry polohy a rozložení=== | ||
[[File:prumer, median, modus.png|400px]] | [[File:prumer, median, modus.png|400px]] | ||
Verze z 28. 11. 2016, 13:15
Obsah
Popisování míry polohy
Upozornění: Tato stránka je poněkud školometská, protože pojednává o základních metodách, které prostě musíme umět a nejsou ničím zábavné. Pokud má laskavý čtenáŕ více času a zvídavosti, nechť se nechá přesměrovat na perfektní vida Khanovy školy, kde mu vše bude vysvětleno zábavněji, než zde :)
Míry polohy slouží k popsání tzv. centrální tendence dané proměnné. Velmi často jde o první ukazatel, který nás zajímá, chceme-li si udělat představu o tom, jak data vypadají. Míry polohy nám dokáží odpovědět na otázky jako: "Jak byli zhruba účastníci studie staří?", nebo "Jaká byla nejčastější známka studentů psychologie ze statistiky?". Jaký statistický ukazatel máme zvolit nám často napoví typ proměnné. Ve specifických případech ovšem volíme ukazatel jiný (příklady jsou uvedeny u konkrétních ukazatelů). [1]
Modus
Modus (angl. mode, značí se ) je nejjednodušším ukazatelem míry polohy. Odpovídá na otázku, jaká hodnota je v souboru nejčastější. Je jediným ukazatelem, který je uplatnitelný pro nominální proměnné (jako je pohlaví, barva očí nebo fakulty na universitě). Můžeme ho ovšem použít i pro data ordinální (známka ze statistiky) a v některých případech i pro kardinální proměnné. Pokud má proměnná více hodnot s nejvyšší četností, uvádíme všechny.
S modem je zpravidla dobré uvést i relativní četnost (frekvenci) nebo percentuální zastoupení. Často se ani modus explicitně neuvádí a místo toho se uvedou pouze relativní četnosti (čtenář či posluchač podle nich snadno vidí, která z hodnot byla nejčastější). To platí především pro takové proměnné, které nemají mnoho různých hodnot. Tak můžeme často číst například: "Ve vzorku bylo 70 % žen (140/200)", nebo "Respondenti byli studenti filosofických (25 %), lékařských (45 %) a právnických (30 %) fakult". Modus nabývá na důležitosti, pokud možných hodnot bylo hodně a nejčastější z nich "válcuje ostatní". Pokud jsme se studentů ptali, jaká byla jejich oblíbená kniha v dospívání, přičemž velká část (20 %) se shodne na "Harry Potter", a zbytek se rozdrobí mezi všechny ostatní tituly (kolem 1 % každá), pak se dá uvažovat o tom, že modus je dobrým popisem centrální tendence. Kdyby ale všechny tituly měly přibližně stejně (kolem 1 %) a "Harry Potter" měl 1,1 %, tradičně vzato je to stále modus, ovšem jeho vypovídající hodnota není tak velká. Z tohoto důvodu je vždy potřeba přemýšlet o tom, co nám vlastně modus říká v konkrétní situaci.
Medián
Medián (angl. median, značí se ) je přesně to, co jeho název napovídá - prostředek hodnot. Je specifickým případem percentilu (50%). Pro zjištění mediánu nejdříve hodnoty seřadíme od největší po největší a hodnota, která leží přesně ve středu, je mediánem. V případě sudého počtu hodnot je medián vypočítán jako aritmetický průměr dvou středních hodnot.
př. Známky ze statistiky byly následující: 1,1,1,1,1,1,2,2,2,3,3. Jedenáct známek, čili prostřední známka znamená medián. V tomto případě jde o známku 1. Jak najít prostřední hodnotu? Jednoduchý postup je vydělit celkový počet hodnot dvěma a přičíst 0,5 (11/2=5,5, po přičtení dostaneme 6 - medián je tedy šestá hodnota v pořadí).
př 2. Co kdyby byly známky jiné? Co třeba: 1,1,1,1,1,1,2,2,2,2,3,3. Počet známek (12) vydělíme dvěma - výsledek 6. Přičteme 0,5, a zjistíme, že medián leží někde mezi šestou a sedmou hodnotou. Vypočteme aritmetický průměr těchto dvou hodnot - v tomto případě (1+2)/2 = 1,5. Medián známek je tedy 1,5.
Všimněte si, že zatímco v prvním příkladě medián je též modus, v druhém případě se tyto ukazatele trochu rozcházejí - modus je stále 1, ovšem medián vzrostl na 1,5.
Jak je patrno z příkladů a definice mediánu, abychom mohli medián vypočítat, potřebujeme takovou proměnnou, kde se hodnoty dají seřadit od nejmenší po největší, čili minimálně ordinální. Někdy se ovšem stává, že ani pro ordinální proměnné není medián příliš užitečný. Např. pokud máme sudý počet lidí v souboru a medián padne přesně mezi lidi, kteří mají ukončené střední vzdělání a ty, kteří mají vysokou školu, jak máme spočítat medián (průměr střední a vysoké školy)? Naštěstí v takových případech můžeme prostě napsat, že polovina účastníků má nejvyšší dosažené vzdělání maximálně střední školu. Ale ani to není tak úplně zajímavé. V případech, jako je tento, bychom se tak pravděpodobně spokojili s údajem o relativním zastoupení jednotlivých stupňů vzdělání.
Velkou výhodou mediánu je ovšem jeho tzv. robustnost. Ta spočívá v tom, že jeho hodnota není ovlivněna odlehlými hodnotami (které jsou spíše výjimky) a v některých případech tak dokáže popsat centrální tendenci mnohem lépe, než průměr. Medián se tak často používá v případech, kdy kvantitativní proměnná má silné zešikmení, či extrémní hodnoty na jedné nebo druhé straně rozložení. Po vysvětlení průměru následují příklady.
Průměr (aritmetický)
Pravděpodobně nejčastěji se ovšem setkáme s aritmetickým průměrem (angl. mean nebo average, značí se ). Ten má zajímavé vlastnosti, které jsou někdy výhodou a někdy prokletím. Co vlastně průměr říká? Je to číslo, které má pro dané hodnoty nejmenší rozptyl. Naštěstí ovšem nemusíme rozptyl počítat, a stačí nám výpočet, který je většině lidí povědomý. Stačí pouze sečíst všechny hodnoty a vydělit je jejich počtem (následuje matematický zápis tohoto postupu):
př. výška basketbalistů v týmu je (v cm) 201, 195, 180, 185, 193. Průměr pak spočítáme takto:
Průměr se používá především na kvantitativní data, ovšem ve výjimečných případech se dá použít na proměnnou ordinální (např. školní známka).
Jednou z vlastností průměru je jeho senzitivita vůči odlehlým hodnotám. V souboru hodnot, kde se vyskytne nějaká extrémní hodnota, tak může zkreslovat. Typickým příkladem je např. průměrný plat. Hodně lidí je na tom většinou podobně , pár lidí se má o trochu lépe či hůře, a pak je tu mála skupina lidí, kteří vydělávají mnohonásobně víc, než ostatní. Těchto pár procent lidí může s průměrem platů zcela zásadně hnout, i když realita je pro většinu zbylých lidí jiná. Pro takový případ se často spokojíme s mediánem, který odlehlou hodnotou není tak zasažen. Další způsob může být tzv. trimmed mean, kde zkrátka ignorujeme určité procento nejzazších hodnot na obou stranách. K dispozici je ovšem spousta dalších metod (spadajících pod takzvané robustní metody, protože odolávají určitým deviacím dat od našich očekávání), ty zde uvedeny nebudou. Pro zvídavého čtenáře ovšem doporučuji mohykána v oblasti robustních metod, Randa Wilcoxe. [2]
Obecně platí, že pokud je rozložení dat symetrické, pak . Pokud se tyto ukazatele výrazně liší, může to být ukazatel toho, že je potřeba data prozkoumat víc zblízka.
Rozvíjení intuice
Zadání
Nyní si ukážeme na několika příkladech jakým způsobem se míry polohy chovají. V této sekci si můžete vyzkoušet zodpovědět na otázky sami, v další sekci se můžete podívat na řešení.
Míry polohy a rozložení
Dokážete říct, která z čar na grafu představuje modus, medián a průměr? Který z ukazatelů je v příkladech vhodný jako ukazatel centrální tendence?