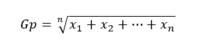Střední hodnota: Porovnání verzí
(Založena nová stránka s textem „Kategorie:Hesla ke zpracování UISK“) |
|||
| Řádek 1: | Řádek 1: | ||
[[Kategorie:Hesla ke zpracování UISK]] | [[Kategorie:Hesla ke zpracování UISK]] | ||
| + | '''Střední hodnota''' je statistická veličina, která se nachází ve středu hledaných hodnot. Pro určování skutečných, nebo-li přesných parametrů se používají řecká písmena a pro výběrové parametry nebo-li odhady skutečných parametrů písmena z latinské abecedy. | ||
| + | |||
| + | == Základní termíny == | ||
| + | |||
| + | === Statistický soubor === | ||
| + | |||
| + | je množina prvků, které jsou předmětem statistického šetření. Pokud je kompletní množinu prvků jedná se o tzv. '''základní soubor'''. Pokud tento základní soubor není k dispozici a je zkoumaná náhodná veličina nebo prvek jedná se o tzv. '''výběrový soubor'''. Počet prvků souboru je '''rozsah souboru'''. | ||
| + | |||
| + | === Základní soubor === | ||
| + | |||
| + | Je zadán přesným vymezením prvků. Prvky mohou být v podobě různým objektů například osoby, zvířata, čísla apod. Počet prvků v tomto souboru může mít rozsah konečný nebo nekonečný. | ||
| + | |||
| + | * Konečný rozsah-sledovaná hodnota je přesně vymezena. | ||
| + | * Nekonečný rozsah-sledovaná hodnota je prakticky vymezena nekonečně (počet prvků je proměnlivý, nelze ho přesně zjistit). | ||
| + | |||
| + | === Výběrový soubor === | ||
| + | |||
| + | Tento soubor je vymezen určitým počtem prvků z výčtu základního souboru, u které se provádí měření zkoumané oblasti. Má být nejlepším představitelem základního souboru tím, že výběr prvků musí být zcela náhodný. '''Náhodný výběr''' znamená, že prvky výběrového souboru (prakticky naměřené hodnoty) jsou vybrány nezávisle, aby všechny prvky základního souboru měly možnost být v tomto výběru zahrnuty. | ||
| + | |||
| + | |||
| + | Střední hodnotu popisuje statistická charakteristika. Dělí tuto střední hodnotu na: | ||
| + | |||
| + | * Průměry - '''aritmetický a geometrický''' | ||
| + | * Další střední hodnoty - '''modus a medián''' | ||
| + | |||
| + | == Aritmetický průměr == | ||
| + | |||
| + | ''μ'' (základní soubor), ''x̅'' (výběrový soubor) | ||
| + | |||
| + | Tato hodnota popisuje přesný parametr ''μ'', tedy skutečný střed (průměr) základního souboru. | ||
| + | Aritmetický průměr určuje průměr výběrového souboru. | ||
| + | |||
| + | '''Definice''' = Součet vybraných náhodných hodnot dělený počtem hodnot stejného výběru. Výsledek toho znamená, že průměr ukazuje část z výběru, která připadá na jednu hodnotu výrazu. Střední hodnota ''μ'' představující přesný parametr je její výpočet možný pouze teoreticky, protože není většinou přesně známá hodnota základního souboru. | ||
| + | |||
| + | Vlastnosti: | ||
| + | * Průměr ovlivňují tzv. extrémní hodnoty. To znamená, že kdy kdykoliv se změní hodnot, tak se mění i průměr souboru. | ||
| + | * Pokud se všechny hodnoty násobí nenulovou konstantou, tak i aritmetický průměr je znásoben touto konstantou. | ||
| + | * Pokud nahradíme hodnoty znaku jejich průměrem, tak se součet souboru nezmění. | ||
| + | * Součet odchylek jednotlivých hodnot od jejich AP je vždy nulový. | ||
| + | |||
| + | Vypočítá se tak, že se sečtou veškeré vybrané prvky a výsledek se vydělí počtem prvků. | ||
| + | |||
| + | Vzorec: | ||
| + | |||
| + | [[File:Aritmetický průměr - vzorec.PNG|150px]] | ||
| + | |||
| + | |||
| + | == Geometrický průměr == | ||
| + | (základní soubor), (výběrový soubor) | ||
| + | Jsou to kladné hodnoty ''x<sub>i</sub>'', které jsou definovány jako ''n''-tá odmocnina ze součinu všech hodnot. Logaritmus geometrického průměru se rovná aritmetickému průměru logaritmovaných hodnot. | ||
| + | |||
| + | Výpočet průměru je stejný jako u aritmetického jen místo sčítání se používá násobení a místo dělení odmocnina. | ||
| + | |||
| + | Vzorec: | ||
| + | |||
| + | [[File:Geometrický průměr - vzorec.PNG|200px]] | ||
| + | |||
| + | == Medián == | ||
| + | (základní soubor), (výběrový soubor) | ||
| + | Hodnota, která se nachází přesně uprostřed všech sledujících hodnot. Hodnoty se musí seřadit podle velikosti a pak se určí střed. Z toho vyplývá, že nezáleží na hodnotě čísla, ale kde se nachází. Hraje zde role, jestli je počet prvků sudý nebo lichý. Pokud nastane situace, kdy je počet vybraných hodnot sudý, medián se zjistí tak, že se vezmou dvě hodnoty zprostřed řady a vypočítá se jejich aritmetický průměr. | ||
| + | |||
| + | == Modus == | ||
| + | (základní soubor), (výběrový soubor) | ||
| + | Hodnota, která se objevuje ve výběru prvků nejčastěji. V tabulce rozdělení četností se určí z hodnoty znaku, která má největší četnost. Modus je tedy konkrétní hodnota, která není přímo ovlivněna velikostí všech hodnot dané proměnné. | ||
Verze z 22. 12. 2018, 17:15
Střední hodnota je statistická veličina, která se nachází ve středu hledaných hodnot. Pro určování skutečných, nebo-li přesných parametrů se používají řecká písmena a pro výběrové parametry nebo-li odhady skutečných parametrů písmena z latinské abecedy.
Obsah
Základní termíny
Statistický soubor
je množina prvků, které jsou předmětem statistického šetření. Pokud je kompletní množinu prvků jedná se o tzv. základní soubor. Pokud tento základní soubor není k dispozici a je zkoumaná náhodná veličina nebo prvek jedná se o tzv. výběrový soubor. Počet prvků souboru je rozsah souboru.
Základní soubor
Je zadán přesným vymezením prvků. Prvky mohou být v podobě různým objektů například osoby, zvířata, čísla apod. Počet prvků v tomto souboru může mít rozsah konečný nebo nekonečný.
- Konečný rozsah-sledovaná hodnota je přesně vymezena.
- Nekonečný rozsah-sledovaná hodnota je prakticky vymezena nekonečně (počet prvků je proměnlivý, nelze ho přesně zjistit).
Výběrový soubor
Tento soubor je vymezen určitým počtem prvků z výčtu základního souboru, u které se provádí měření zkoumané oblasti. Má být nejlepším představitelem základního souboru tím, že výběr prvků musí být zcela náhodný. Náhodný výběr znamená, že prvky výběrového souboru (prakticky naměřené hodnoty) jsou vybrány nezávisle, aby všechny prvky základního souboru měly možnost být v tomto výběru zahrnuty.
Střední hodnotu popisuje statistická charakteristika. Dělí tuto střední hodnotu na:
- Průměry - aritmetický a geometrický
- Další střední hodnoty - modus a medián
Aritmetický průměr
μ (základní soubor), x̅ (výběrový soubor)
Tato hodnota popisuje přesný parametr μ, tedy skutečný střed (průměr) základního souboru. Aritmetický průměr určuje průměr výběrového souboru.
Definice = Součet vybraných náhodných hodnot dělený počtem hodnot stejného výběru. Výsledek toho znamená, že průměr ukazuje část z výběru, která připadá na jednu hodnotu výrazu. Střední hodnota μ představující přesný parametr je její výpočet možný pouze teoreticky, protože není většinou přesně známá hodnota základního souboru.
Vlastnosti:
- Průměr ovlivňují tzv. extrémní hodnoty. To znamená, že kdy kdykoliv se změní hodnot, tak se mění i průměr souboru.
- Pokud se všechny hodnoty násobí nenulovou konstantou, tak i aritmetický průměr je znásoben touto konstantou.
- Pokud nahradíme hodnoty znaku jejich průměrem, tak se součet souboru nezmění.
- Součet odchylek jednotlivých hodnot od jejich AP je vždy nulový.
Vypočítá se tak, že se sečtou veškeré vybrané prvky a výsledek se vydělí počtem prvků.
Vzorec:
Geometrický průměr
(základní soubor), (výběrový soubor)
Jsou to kladné hodnoty xi, které jsou definovány jako n-tá odmocnina ze součinu všech hodnot. Logaritmus geometrického průměru se rovná aritmetickému průměru logaritmovaných hodnot.
Výpočet průměru je stejný jako u aritmetického jen místo sčítání se používá násobení a místo dělení odmocnina.
Vzorec:
Medián
(základní soubor), (výběrový soubor)
Hodnota, která se nachází přesně uprostřed všech sledujících hodnot. Hodnoty se musí seřadit podle velikosti a pak se určí střed. Z toho vyplývá, že nezáleží na hodnotě čísla, ale kde se nachází. Hraje zde role, jestli je počet prvků sudý nebo lichý. Pokud nastane situace, kdy je počet vybraných hodnot sudý, medián se zjistí tak, že se vezmou dvě hodnoty zprostřed řady a vypočítá se jejich aritmetický průměr.
Modus
(základní soubor), (výběrový soubor)
Hodnota, která se objevuje ve výběru prvků nejčastěji. V tabulce rozdělení četností se určí z hodnoty znaku, která má největší četnost. Modus je tedy konkrétní hodnota, která není přímo ovlivněna velikostí všech hodnot dané proměnné.