Shannon-Fanovo kódování: Porovnání verzí

Řádek 57: Řádek 57:
 
<table>
 
<table>
 
<tr>
 
<tr>
−
<td>
+
<td> A)
 
{| class="wikitable"
 
{| class="wikitable"
 
|-
 
|-
Řádek 76: Řádek 76:
  
 
</td>
 
</td>
−
<td>
+
<td> B)
  
 
{| class="wikitable"
 
{| class="wikitable"
Řádek 96: Řádek 96:
  
 
</td>
 
</td>
−
<td>
+
<td> C)
  
 
{| class="wikitable"
 
{| class="wikitable"
Řádek 116: Řádek 116:
  
 
</td>
 
</td>
−
<td>
+
<td> D)
  
 
{| class="wikitable"
 
{| class="wikitable"
Řádek 136: Řádek 136:
  
 
</td>
 
</td>
−
<td>
+
<td> Konečná verze
  
 
{| class="wikitable"
 
{| class="wikitable"
Řádek 158: Řádek 158:
 
</tr>
 
</tr>
 
</table><ref name="voho"/>
 
</table><ref name="voho"/>
 +
 +
 
'''''Krok 1''''' = Rozdělit na dvě poloviny s přibližně stejným součtem četností
 
'''''Krok 1''''' = Rozdělit na dvě poloviny s přibližně stejným součtem četností
 
* (F,D) - součet četností: 5 + 4 = 9
 
* (F,D) - součet četností: 5 + 4 = 9

Verze z 26. 1. 2019, 12:38

Shannon-Fanovo kódování je technika pro sestavení prefixového kódu založená na seznamu symbolů a počtech jejich výskytů v roce 1949 metodu nezávisle na sobě publikovali Claude Elwood Shannon (otec teorie informace)[1] s Warrenem Weaverem a Robertem Mario Fano.[2]

  • Řešení nemusí být vždy optimální (nejkratší)
  • Používá se v kompresních datech [3]
  • Asymetrická kompresní metoda
  • Dvouprůchodová kompresní metoda
  • Semi-adaptivní kompresní metoda
  • Dosahuje horších výsledků ve srovnání s Huffmanovým kódováním [1]
C.E.Shannon

C.E.Shannon

Časová a paměťová složitost algoritmu

  • Časová složitost algoritmu: O(n + |Σ| * log|Σ|)
  • Paměťová složitost algoritmu: O(|Σ|)

Z uvedeného popisu algortimu plynou následující fáze. Z hlediska časové složitosti je zde fráze výpočtu četnosti jednotlivých znaků, lineárně závislá na délce vstupního textu. Dále fáze seřazení znaků, závislá na použitém adícím algoritmu. Následuje generování výstupu, též lineárně závislé na délce vstupního textu. Paměťová složiost roste lineárně s počtem různých znaků ve vstupu.[1]

Konstrukce binárního kódu

Princip je založen na množině znaků rekursivně dělících se vždy na dvě podmnožiny, aby součet výskytů znaků v obou podmnožinách byl přibližně stejný. Jedné podmnožině je pak v kódu přiřazena binární 1 a druhé 0.[4]

  • Postup není optimální
  • Důležitá vlastnost: opětovné prefixovost


Prefixovost Shannon-Fanova kódu můžeme zachytit binárním prefixovým stromem. Písmena vstupní abecedy jsou v listech a jejich kódy tvoří od cesta od kořene do daného vrcholu.

  • Neprefixový kód = na cestě do nějakého listu leží nějaké písmeno vstupní abecedy. [5]

Pseudokód

  1. Pro danou zprávu vytvořit seznam symbolů a zjistit počet jejich výskytů (nebo pravděpodobnost)
  2. Seznam symbolů seřadit do neklesající posloupnosti podle této hodnoty
  3. Kódy všech symbolů jsou zpočátku prázdné
  4. Rozdělit seznam na dvě poloviny tak, aby součet sledovaných hodnot byl v obou částech zhruba stejný
  5. Ke kódům symbolů levé polovině připojit 0, ke kódům symbolů v pravé polovině připojit 1
  6. Rekurzivně opakovat od kroku 4 na levou i pravou polovinu seznamu [2]

Příklady

příklad 1)

Symbol Počet výskytů
F 5
D 4
C 4
A 3
B 3
E 2

Inicializace Seznam je (F,D,C,A,B,E). Kódy všech symbolů jsou prázdné.

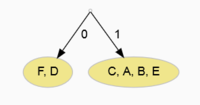
A)
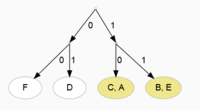
Symbol Kód
F -
D -
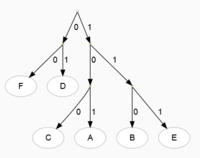
C -
A -
B -
E -
B)
Symbol Kód
F 0
D 0
C 1
A 1
B 1
E 1
C)
Symbol Kód
F 0 0
D 0 1
C 1 0
A 1 0
B 1 1
E 1 1
D)
Symbol Kód
F 0 0
D 0 1
C 1 0 0
A 1 0 1
B 1 1 0
E 1 1 1
Konečná verze
Symbol Kód
F 0 0
D 0 1
C 1 0 0
A 1 0 1
B 1 1 0
E 1 1 1

[2]


Krok 1 = Rozdělit na dvě poloviny s přibližně stejným součtem četností

  • (F,D) - součet četností: 5 + 4 = 9
  • (C,A,B,E) - součet četností: 4 + 3 + 3 + 2 = 12
Symbol Kód
F 0
D 0
C 1
A 1
B 1
E 1

1.PNG

Krok 2 = Nyní oba seznamy rozdělit na poloviny s přibližně stejným součtem četostí

Symbol Kód
F 0 0
D 0 1
C 1 0
A 1 0
B 1 1
E 1 1

2.PNG

Krok 3 = Seznamy (F) a (D) již rozložit nejdou, zbývá zpracovat seznamy (C,A) a (B,E). Opět oba rozložit na poloviny s přibližně stejným součtem četností.

Symbol Kód
F 0 0
D 0 1
C 1 0 0
A 1 0 1
B 1 1 0
E 1 1 1

3.PNG

Výsledek

Symbol Kód
F 0 0
D 0 1
C 1 0 0
A 1 0 1
B 1 1 0
E 1 1 1

[2]

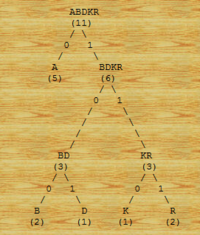
příklad 2)

  • Vstupní soubor: ABRAKADABRA
  • Jednotlivé znaky: A B D K R
  • Počty výskytů: (5) (2) (1) (1) (2)
  • Vytvořený strom:

Strom.PNG[6]

Odkazy

Reference

  1. ↑ 1,0 1,1 1,2 Shannon-Fanovo kódování. Dostupné také z: http://www.stringology.org/DataCompression/sf/index_cs.html
  2. ↑ 2,0 2,1 2,2 2,3 Shannon-Fanovo kódování. Dostupné také z: http://voho.eu/wiki/kodovani-shannon-fano/
  3. ↑ Teorie kódování: Shannon-Fanova metoda. Praha: Konrád Černý. Dostupné také z: https://files.klaska.net/sites/files.klaska.net/files/manual_files/cvut/Teorie kodovani/Shannon-Fanovo k_dov_n_.pdf
  4. ↑ Optimální (entropické) kódování informačního zdroje. Dostupné také z: https://wikisofia.cz/wiki/Optimální_(entropické)_kódování_informačního_zdroje
  5. ↑ RADOMIL, Matoušek. Metody kódování. Brno, 2006, 96 s. Dostupné také z: http://www.uai.fme.vutbr.cz/~matousek/TIK/TIKv19.pdf
  6. ↑ Shannon-Fanovo kódování. Dostupné také z: https://atrey.karlin.mff.cuni.cz/~tnovak/compress/huffman/shannon.html

Související články

Optimální (entropické) kódování informačního zdroje

Huffmanove kódovanie

Kódování

Klíčová slova

kódování, Shannon, Fano, Shannon-Fanovo kódování

Citováno z „https://wikisofia.cz/w/index.php?title=Shannon-Fanovo_kódování&oldid=57031“