Konstrukce rozhodovacích stromů (princip snižování entropie)

Rozhodovací stromy

Nejčastěji se koncept rozhodovacích stromů používá v oblasti výpočetní techniky. Tato metoda spadá mezi metody dobývání znalostí, jejichž cílem je dojít informacím za pomoci předem získaných dat a nalézt v datech vzájemné závislosti. Rozhodovací stromy vizuálně znázorňují celý proces rozhodování a cestu ke správnému výsledku. Všechny možnosti, dotazy a odpovědi jsou vidět zároveň.

Struktura

popis konstrukce rozhodovacího stromu

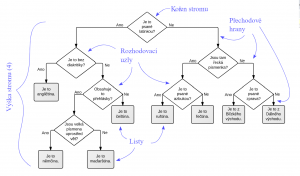
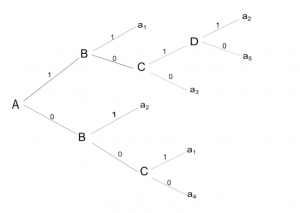
Základem (počátek dotazu) je výchozí uzel, tzv. kořen stromu. Obsahuje první otázku. Podle získané odpovědi pokračujeme po odpovídající hraně do příslušného podstromu a tak dál, až dojdeme ke konečné odpovědi. Ta je zapsaná v tzv. listu, tedy uzlu, ze kterého nevedou další hrany (protože neklade další otázky). Počet úrovní stromu od kořene k nejzazšímu listu nazýváme výškou stromu.

• Kořen stromu, je uzel do nějž nevstupují žádné hrany, do

ostatních uzlů vstupuje právě jedna hrana.

• Terminální uzly (listy stromu) jsou ty vrcholy, z nichž žádná hrana

nevystupuje.

• Neterminálním (rozhodovacím) uzlům jsou přiřazeny otázky Q1,...,Qn tak, že na

žádné cestě z kořene se nesmí žádná otázka opakovat.

• z každého neterminálního uzlu vycházejí orientované (přechodové) hrany (větve)

označené jednotlivými možnými odpověďmi na přiřazenou otázku.

• terminálním uzlům jsou přiřazena rozhodnutí.

Princip snižování entropie

Informace

Pojem informace má mnoho definic, ovšem z pohledu rozhodování je nejpříhodnější ji definovat jako úbytek entropie(neboli možností). Každá další informace v rozhodovacím stromě nás přiblíží ke správnému rozhodnutí tak, že ubyde naše nevědomost v rámci problematiky a tím i možnosti v rozhodování.

Entropie

Entropie, neboli chaos. Míra entropie vyjadřuje například míru nevědomosti, neuspořádanost systému, šum v přenosu dat či nedostatek informační hodnoty ve sdělení. Čím víc máme informací k danému tématu, otázce, problému, tím se snižuje míra entropie.