Základy reprezentace trojrozměrného prostoru v počítači

Matematický základ počítačového přístupu

Trojrozměrný (3D) prostor může na úrovni digitálního vstupu, zpracování či výstupu nabývat různé komplexity, věrohodnosti a s ní spojeným pocitem imerze; to vše v závislosti na prostředcích a metodách užitých na jednotlivých úrovních. Počítač je de facto matematickým nástrojem a jelikož matematika umožňuje vytvářet konstrukce přesahující lidskou smyslovou zkušenost, může počítačový program pracovat s jakýmkoliv prostorem, disponuje-li jeho použitelným modelem. Takový model pak musí nutně pracovat s kvantifací.

Ponecháme-li stranou geometrii, jež sama představuje pouze dílčí součást matematiky, každý si snadno představí čtvrtý rozměr jakožto čas, pátý například jako teplotu atd. Čas jako rozměr je v podobě časové osy nezbytnou součástí každého animačního softwaru, s teplotou se musí počítat ve speciálních konstruktérských programech při výpočtech namáhání materiálů během jejich styku s okolím. Avšak i geometrii dejme tomu pátého rozměru lze počítačem modelovat - ať už existuje v realitě našeho vesmíru či nikoliv. Je totiž kvantifikovatelná a tudíž přístupná počítači. Pro lidské smysly je však nejpřístupnější 3D prostor (zrak, hmat či sluch jsou na něj adaptovány), a proto zaujímá 3D přístup v počítačovém zpracování prostoru přední postavení – samozřejmě společně s výpočetně obecně méně náročnější 2D oblastí.

Kartézská soustava souřadnic jako základ 3D geometrie

Ať už chceme 3D prostor v počítači definovat za účelem studia zvuku či obrazu, musíme disponovat použitelným modelem k reprezentaci vytvářených či upravovaných objektů ve třech rozměrech, jimiž jsou délka, šířka a hloubka (či výška). Takový model existuje a vychází z kartézské soustavy souřadnic, kterou v 17. století formuloval francouzský filosof a matematik René Descartes. Její pomocí se mu podařilo propojit euklidovskou geometrii s algebrou.

Tři zmíněné rozměry mají v modelu podobu os konvenčně označovaných písmeny x, y a z. Každá ze tří dvojic těchto os tvoří rovinu, jež je v trojrozměrném prostoru kolmá (ortogonální) na zbývající dvě. Bod v prostoru (základní jednotka počítačového zpracování trojrozměrného prostoru) je pak definován polohou na každé ze tří os. Samotná poloha je vyjádřena pomocí číselné hodnoty – např. Souřadnice (1, -1, 7) vypovídá o bodu tolik, že leží 1 jednotku od počátku na ose x, -1 jednotku od počátku na ose y a 7 jednotek od počátku na ose z. Počátkem, lépe řečeno středem prostoru je nula, jež je prostorově společná pro všechny tři osy.

Negativních hodnot je zapotřebí pro vyjádření opačných směrů na jednotlivých osách. Souřadnice (0, 0, 0), tedy absolutní střed 3D prostoru, doplněná o pozitivní i negativní směry a jejich kombinace umožňuje takové zaplňování prostoru objekty, které není omezeno v žádném směru; může pokračovat do nekonečna, limitujícím faktorem je v praktickém nasazení pouze paměť počítače. Koncepce kartézské soustavy souřadnic a její využití v počítačovém zpracování 3D prostoru jsou patrné z následujících dvou obrázků.

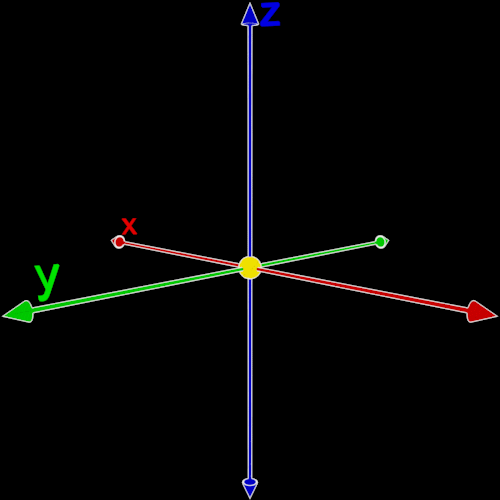
Obrázek 1.1: Trojrozměrný prostor definovaný třemi osami kartézské soustavy souřadnic; žlutá koule značí střed prostoru s polohou (0, 0, 0).

Obrázek 1.2: Trojice bodů v prostoru kartézské soustavy souřadnic; každý bod je doplněn popiskem, jenž vyjadřuje jeho přesné umístění ve formátu (x, y, z); pro přehlednost je zobrazena pouze osmina prostoru.

Různé způsoby reprezentace prostorových objektů

Souřadnice určené trojicí číselných hodnot jsou základem „zhmotnění“ jakéhokoliv geometrického obsahu ve 3D prostoru. Reprezentace tohoto obsahu ovšem není pouze jediná. Existují tři základní metody.

Hraniční reprezentace

Tento způsob reprezentace popisuje pouze povrch objektu, nikoliv jeho vnitřní stav. Určuje, kde leží hranice mezi objektem a okolním prostorem. Pomocí 3D modelovacího softwaru vytváříme jakoby obálku či „skořápku“ objektu, na níž můžeme posléze například aplikovat barvu v podobě textury.

V celém hraničním přístupu existuje několik způsobů zápisu povrchu těles:

parametrické plochy – objekt se skládá z elementárních ploch, jež jsou vyjádřeny bodovými rovnicemi

křivky NURBS – definice objektu využívá tzv. NeUniformních Racionálních B-křivek. Díky nim lze s velice malými paměťovými nároky docílit i komplikovaných zaoblení.

surfely (orientované rovinné plošky) - poměrně exotická metoda

polygonální síť – nejrozšířenější způsob zápisu 3D objektů. Každý polygonálně definovaný prostorový objekt se skládá z uspořádané skupiny spojených rovinných n-úhelníků, neboli polygonů. Ty jsou tvořeny minimálně trojicí bodů, neboť nejjednodušším plošným útvarem je trojúhelník. Častěji se ovšem využívají obdélníky. Polygonální hraniční reprezentace dominuje především v zábavní sféře, ať už jde o modely pro filmy či počítačové hry. Především 3D počítačové hry, tedy takové, jež využívají hardwarové grafické akcelerace pomocí rozhraní DirectX či OpenGL, vyžadují polygonové modely, neboť pouze ty mohou být akcelerovány současným široce dostupným hardwarem a tím pádem prezentovány v rychlosti, jež nenaruší pocit imerze ve virtuálním světě.

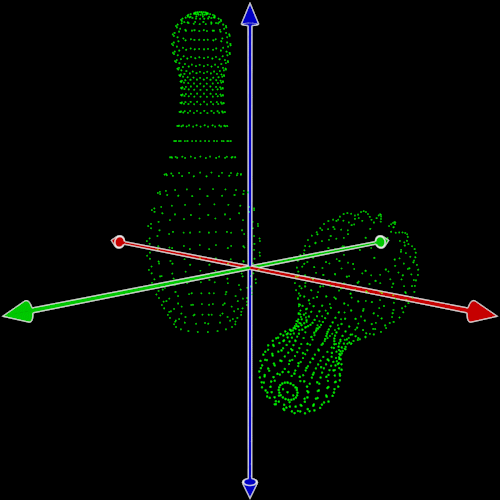
Obrázek 2.1: Tzv. bodové mračno složené z povrchových bodů tělesa zapsaného pomocí hraniční reprezentace

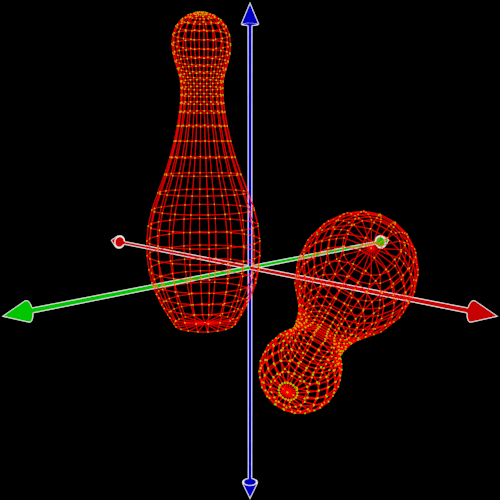
Obrázek 2.2: Hranice jednotlivých dílčích ploch tělesa – polygonů. V tomto případě vyjádřené čtveřicemi či trojicemi (dno kuželky) bodů.

Obrázek 2.3: Po vyplnění jednotlivých ohraničení v rámci sítě získáme plochy. Každá plocha má svoji normálu, která určuje, odkud přichází na povrch světlo, a kam se následně odráží.

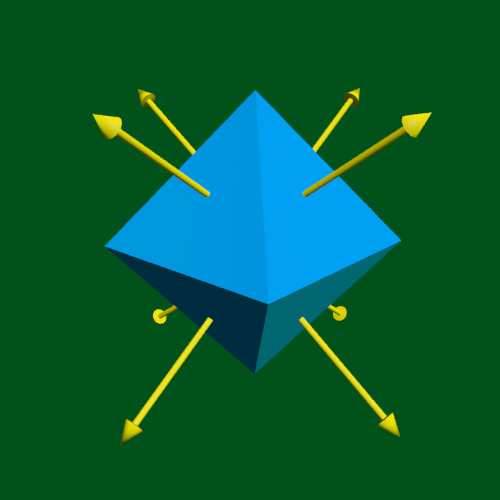
Obrázek 2.4: Tzv. normály, neboli normálové vektory. Tyto pomyslné kolmice na jednotlivé plochy (v tomto případě 8 trojúhelníků) tělesa určují, která strana plochy je vnitřní a která naopak vnější, tedy přijímající a odrážející světlo.

Obrázek 2.5: Normály jsou důležité pro výpočet hladkého povrchu. V tomto případě zůstal zachován stejný počet polygonů jako na obrázku 2.3, ke stínování objektu však nebyly použity normály dílčích ploch, ale normály jednotlivých bodů, jež byly určeny zprůměrováním normál přiléhajících ploch. Z předchozích obrázků je patrné, že každý bod definující povrch kuželky je společný pro 4 polygony (s výjimkou středového bodu na špičce a na dně).

Obrázek 2.6: Objekty definované pomocí křivek NURBS

Objemová reprezentace

Objemová reprezentace prostorových objektů pracuje s informací, zda je určitý bod 3D prostoru součástí daného objektu či nikoliv. Vedle povrchu tedy popisuje i objem těles. Objemová reprezentace je nutná ve chvíli, kdy např. chceme zjistit, kolik tepelné energie projde zahřívaným kovovým blokem o tloušťce 1 cm apod. Obecně se s objemovou reprezentací setkáme spíše v technických oblastech či medicíně, neboť pro estetické účely většinou plně postačí hraniční reprezentace.

Také objemová reprezentace není omezena pouze na jediný přístup, jak objekty definovat. Nabízí tři odlišné metody:

Konstruktivní geometrie těles (CSG) – základem zápisu těles je vzájemné kombinování více jednodušších objektů prostřednictvím Booleových množinových operací. Kombinací může být například odečtení objemu jednoho tělesa od druhého.

Vyčíslení objemu obsazeného tělesem – prostor je rozdělen na objemové bloky, tzv. voxely, které slouží jako základní jednotka prostoru. Jednotlivým voxelům lze připsat například rozdílnou hustotu, lom světla či jeho propustnost apod. Voxelová metoda má svůj původ v medicíně – vzešla z potřeby zobrazit data získaná z přístrojů pro CT či magnetickou rezonanci v přehledné podobě. Je vhodná i pro běžné modelování, kde dokáže za krátký čas získat komplikované tvary. Softwarová podpora však není tak bohatá jako u polygonálního modelování. Jisté problémy s sebou voxely přinášeji i v oblasti animace, naštěstí lze voxelové modely převádět na polygonální reprezentaci.

Implicitní plochy – známé spíše jako blobs či metaballs. Základem tělesa jsou jednotlivé body prostoru představující středy koulí, které při vzájemném prolínání vytvářejí složitější tělesa. Tato metoda nachází uplatnění u komplikovaných úloh typu zobrazení kapalin v pohybu.

Obrázek 2.7: Několik jednoduchých geometrických objektů, jejichž kombinací metodou CSG můžeme podle zvolených typů Booleových operací získat různé výsledky.

Obrázek 2.8: Objem trojice válců a čtveřice dlouhých kvádrů byl odečten od objemu velkého kvádru. Ten byl navíc doplněn o vyčnívající část původní koule.

Obrázek 2.9: Reprezentace objektů prostřednictvím voxelů (jednotlivých buněk prostorové mřížky). Voxely nemusí mít nutně krychlový tvar.

Obrázek 2.10: Tytéž objekty umístěné do voxelové mřížky s vyšším rozlišením

Obrázek 2.11: Voxelové modelování v nástroji 3D-Coat. Hladkého vykreslování hrubých voxelů je dosaženo jejich polynomiální interpolací.

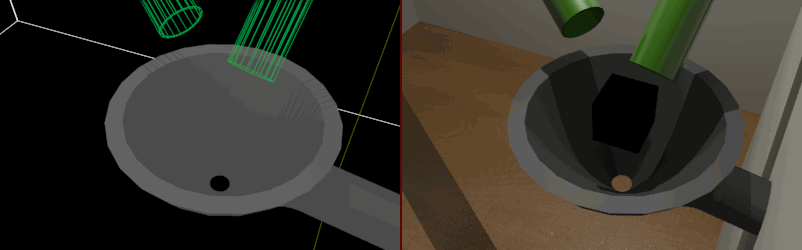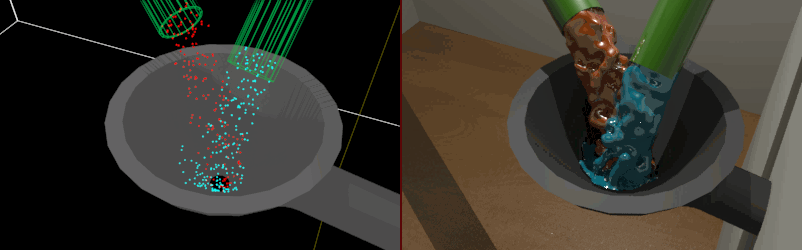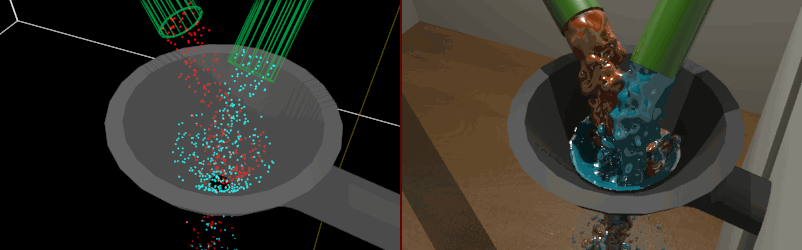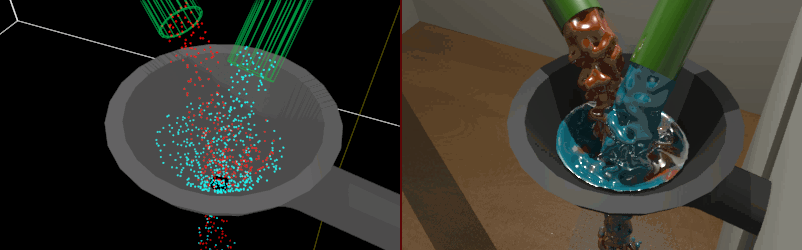
Obrázek 2.12: Vizualizace kapalin pomocí metaballs. Levá část animace znázorňuje výchozí bezrozměrné body pro konstrukci objemu.

Procedurální reprezentace

Tělesa jsou definována algoritmy. Uživatel upřesní několik parametrů a program následně automaticky vytvoří objekt. Při generování lze použít například fraktály, výsledné tvary tak mohou být velmi komplexní.

Obrázek 2.13: Procedurálně reprezentovaný model pohoří

Mapy a textury aneb záchrana před nadměrným modelováním

Při vytváření 3D objektu je třeba přiřadit mu určitou barvu, abychom jej vůbec viděli. Jedna barva na jeden objekt, případně na jeho samostatnou část, zvyšuje přehlednost, a proto se tento přístup s oblibou využívá zejména v oblasti počítačem podporovaného projektování (CAD = Computer Aided Design). Mimo primárně technickou oblast využití je však z estetického hlediska nutné, aby povrchy objektů obsahovaly různé podrobnosti. Někdy jich je zapotřebí tolik, že dělení objektu na velmi malé části za účelem jejich následného přímého obarvování zvolenými barvami by bylo naprosto nepraktické - jak z hlediska lidského času, tak systémových prostředků. Aby tedy nebylo zapotřebí zacházet při modelování 3D objektů do absurdních detailů, používají se textury neboli mapy.

Mapy zahalí povrch tělesa, a jednotlivým jeho oblastem tak přidají detail určitého druhu. Detailem může být například barva, kterou vidíme po osvětlení dané části tělesa bílým světlem. Jde o tzv. difúzní barvu, na kterou se ptáme otázkou „Jakou má ta věc barvu?“. Difúzní barva tvoří obsah nejčastěji používaných map.

Obrázek 3.1: Nakreslení kruhu na těleso lze provést dvěma způsoby. Vlevo: Je možné sestoupit na úroveň geometrického popisu, přidat nové polygony (používáme-li polygonovou reprezentaci) a ty pak jednotlivě obarvit. Výsledkem ovšem mohou být nesladěné normály a často velký nárůst polygonů, jenž se objeví především ve chvíli, kdy se snažíme zastřít neřešitelnost kvadratury kruhu, jako je tomu právě v případě křivých tvarů. Vpravo: Mnohem elegantnější metodu představují mapy. V tomto případě byla na objekt namapována 2D difúzní mapa v běžném bitmapovém formátu JPEG. Relativně uspokojivé zakřivenosti kruhu bylo dosaženo bez jakéhokoliv navýšení počtu polygonů.

Použitelnost map se však nevztahuje pouze na difúzní barvu. Mapami lze jednotlivým částem povrchu tělesa přiřadit míru či barvu odlesku, barvu v neosvětleném stavu, průhlednost, průsvitnost, lom světla, vnitřní svítivost, odrazivost a řadu dalších vlastností používaných při popisu povrchu. Mapy je možné na sebe vrstvit, přičemž lokální změny v míře vrstvení lze řídit opět mapou v podobě masky.

Důležitou třídu map představují tzv. bump mapy. Ty vytvářejí iluzi nerovností na povrchu, která působí věrohodně především při kolmém pohledu. Iluze je dosaženo bez navýšení počtu geometrických detailů 3D modelu, neboť využívá mapou řízené lokální vychylování normál od vektoru mateřské plochy. Standardní, nejstarší typ bump mapy využívá k zápisu orientace normál odstíny šedi. Pokročilejší způsob bump mappingu, tzv. normálová mapa, informaci o odchylkách kóduje v RGB obrázku, kde jednotlivé barevné kanály nesou postupně informaci o orientaci normálového vektoru v osách x, y, a z. O něco věrohodnější iluzi hloubky na plošných polygonech pak přináší zatím ne zcela zavedená paralaxní mapa. Bump mapy nacházejí největší uplatnění ve virtuálních simulacích a počítačových hrách, neboť umožňují dosáhnout uspokojivých detailů bez snížení plynulosti pohybu ve virtuálním světě.

Obrázek 3.2: Využití normálové mapy pro dosažení iluze hloubkového detailu na plošném povrchu. Při tomto pohledu v úhlu zhruba 45° je zřejmé, že v případě relativně extrémních hloubek (kříž) už normálová mapa nemůže přinášet zázraky. Mnohem lepší výsledek by se dostavil při čelném pohledu na náhrobní desku. Nemá-li však pozorovatelka možnost srovnání s původním modelem, nemusí si podivnosti iluze ani všimnout. To platí zejména ve chvíli, kdy virtuální svět nenavštívila primárně za účelem pozorování aplikace textur.

nanášení map na objekty

Mapy lze dělit nejenom podle jejich účelu při tvorbě povrchu objektu, ale také podle způsobu, jak jsou reprezentovány v počítači.

První dělení rozlišuje bitmapy a procedurální mapy. Bitmapa je klasická uzavřená 2D textura. Procedurální mapa je generována počítačem na základě algoritmu podobně jako procedurální geometrie. Jednoduchým příkladem procedurální mapy je šachovnicová mapa.

Druhé dělení rozlišuje 2D a 3D mapy. Bitmapové soubory (BMP, TIFF, TGA, PNG, JPEG...) jsou vždy plošné - tedy 2D. Plošná je například i zmíněná procedurální mapa šachovnice. 3D mapy jsou vždy procedurální a respektují vnitřní stavbu tělesa. Umějí například simulovat prostorový kouř, či žilkování mramoru nebo dřeva.

Obrázek 3.3: Procedurální 3D mapa dřeva s procedurálním 3D mramorem na procedurální 2D šachovnici. Při použití 3D map odpadají starosti, jak věrohodně zabarvit povrch s ohledem na vnitřní strukturu materiálů. Např. letokruhy ve kmeni jsou korektně zobrazeny na všech dílčích plochách modelu. 2D mapa založená na fotografii dřeva by sice poskytla více detailů, pokud by ovšem měla respektovat vnitřní strukturu tělesa, byla by její aplikace velmi složitá a náročná.

V praxi tvoří dominantní část map jejich 2D verze. Ty je skoro pokaždé zapotřebí nanést na značně členité povrchy 3D objektů. K tomuto účelu se používá projekce mapy formou tzv. UV mapování, při němž se 3D objekt zapsaný v systému os x, y, z rozkládá do 2D prostoru popsaného osami u a v. Pokročilejší metodu představuje UVW mapování využívající tří os. Kdo pamatuje papírové modely z časopisu ABC, dokáže si celou věc rychle představit. Jelikož ale přenášení 2D plochy na nerovinné 3D útvary s sebou vždy nese určitou míru zkreslení - jak dobře ilustruje historie kartografie - je zapotřebí jít při UV mapování cestou kompromisů. Ve 3D grafice se s oblibou používá 2D procedurální mapa se vzorkem šachovnice, jejíž jednotlivá políčka napovídají, jak velké zkreslení mapa dané oblasti povrchu objektu má. Kompromisy pak mají podobu rozdělení objektů na části s vlastním UV namapováním. 3D map se tento nedostatek netýká.

Obrázek 3.4: Způsob nanášení 2D map na složité 3D objekty. Objekt je rozdělen na několik částí, jak ukazuje UV šablona vlevo dole. Čtvrtiny vpravo nahoře a dole znázorňují difúzní a normálovou mapu, které jsou na objekt naneseny pomocí UV šablony, aby mohl každý detail přijít na zamýšlené místo.

Vizuální výstup prostorových dat – rendering

Počítačová zpracování prostorových dat má několik uplatnění. Slouží jako numerický model pro různé mechanické a jiné fyzikální analýzy, řídí práci elektronických obráběcích strojů při tzv. počítačové podpoře obrábění (CAM = Computer Aided Manufacturing), nebo dovoluje vytvářet vizualizace těchto dat. Využití vizualizace neustále roste. Způsob jakým z dat uchovaných v počítači vzniká obraz či sekvence obrazů nese označení rendering či renderování. Proces renderování lze opět rozdělit podle odlišných kritérií.

První dělení se týká rychlosti renderování a rozlišuje dva přístupy:

Rendering v reálném čase – data jsou vizualizována tak rychle, že vzniká iluze plynulosti. Pro to je potřeba vykreslit alespoň 20 až 30 snímků za sekundu. Příkladem jsou počítačové hry nebo systémy pro virtuální realitu. Při renderingu v reálném čase se ve většině situací nepodílí na výpočtech obrazu pouze CPU. Hlavní část zátěže má totiž na starosti GPU grafického akcelerátoru, jež je uzpůsobené na určité výpočetní operace.

Pre-rendering – vizualizace dat neslouží pro okamžitý výstup na zobrazovací zařízení, nýbrž do samostatného souboru pro pozdější využití. Vykreslování jediného snímku vyžaduje v závislosti na mnoha faktorech sekundy až dny. Mezi tyto faktory patří především použitý model osvětlení scény, složitost použitých map a geometrie objektů, výstupní rozlišení obrazu, efekty typu hloubka ostrosti či rozmazání obrazu ve stylu pohybu kamery a v neposlední řadě výpočetní síla CPU. Výsledky tohoto typu renderování se používají ve filmech, vizualizacích navrhovaných architektonických postupů apod.

Druhé dělení se vztahuje na ambice renderovacího softwaru přiblížit výsledek vzhledu reálného světa (případně jeho percepci lidským zrakem) a rozlišuje dva přístupy:

Fotorealistické renderování – snaží se napodobit skutečné světlo se všemi jeho fenomény, jako je lom, slábnutí se vzdáleností od zdroje apod.

Umělecké renderování – cílem je vykreslení scény v určitém výtvarném stylu. Může jít např. o jednoduché komiksové zvýraznění obrysů pomocí linky, vykreslení uhlem, pointilismus apod.

Rendering lze rozdělit rovněž podle 3D schopností zobrazovacího zařízení:

-Většina soudobé produkce je zobrazována jakoby pro jedno oko (jeden virtuální objektiv kamery) na klasickém 2D výstupním zařízení typu monitoru či papíru – v takovém případě se renderuje z 3D prostoru na 2D plochu pomocí perspektivní či ortogonální projekce.

-V současnosti stoupá podíl stereoskopického renderování s tím, jak roste dostupnost pomocných zařízení (brýle).

-Prostorově nejvěrnější podání 3D dat však slibují až tzv. volumetrické (objemové) displeje umožňující nahlížení scény z libovolného úhlu. Tato oblast je prozatím předmětem výzkumu. Renderování může mít v tomto případě například podobu laserem vyvolaného vzniku plazmatu v části ohraničeného objemu, jež odpovídá určitému voxelu ve zdrojovém počítačovém modelu.

Obrázek 4.1: Nefotorealistické, komiksové vyrenderování jednoduché 3D scény

Obrázek 4.2: Stejná scéna ve fotorealističtějším podání