Současné trendy v psychologické metodologii
Obsah
Síťové modely
Síťové modely jsou v současnosti významnou a rozvíjející se metodou psychometrie. Představují alternativu ke klasickým latentním modelům, ve kterých jsou na základě různých metod estimace vytvářeny hypotézy o existenci latentních proměnných stojících za vztahy mezi manifestními proměnnými (např. pozorovatelné chování nebo položky v testu). Cílem latentních modelů je redukovat manifestní proměnné na menší množství latentních proměnných, které se odvozují a odhadují ze vztahů mezi nimi. Způsoby modelování vztahů mezi psychologickými rysy a pozorovatelnými proměnnými pak můžeme rozdělit na reflektivní a formativní. Reflektivní modely předpokládají existenci latentní proměnné, která je příčinou pozorovatelných proměnných (např. neuroticismus způsobuje obavy, že se stane něco špatného). Formativní model považuje daný latentní rys za výsledný společný efekt proměnných, které tak jsou jednotlivými aspekty daného latentního rysu (např. obavy, že se stane něco špatného utvářejí neuroticismus).[1]
Na rozdíl od tohoto přístupu není předmětem síťových modelů nalézt a pojmenovat latentní proměnné. Manifestní proměnné jsou místo toho považovány za samostatné kauzální jednotky síťového systému, které jsou přímo propojené. V rámci síťových modelů jsou tedy zkoumány vzájemné interakce přímo mezi těmito pozorovatelnými proměnnými a důležitost jednotlivých proměnných pro vysvětlení zkoumaného psychického rysu.[1]
V klasickém modelu bychom mohli například za symptomy únavy, nespavosti, zvýšených obav a potíží se soustředěním hledat depresi jako latentní proměnnou. V síťovém modelu však zůstáváme u těchto manifestních proměnných, které se společně mohou vyskytovat a vzájemně ovlivňovat bez ohledu na existenci nějaké konkrétní latentní proměnné. Vzniká zde kauzální řetězec symptomů, kdy např. nespavost způsobuje únavu, ta vede k potížím se soustředěním vedoucím ke zvýšeným obavám, což vede opět k nespavosti.[1] Jiným příkladem může být situace z pracovní psychologie, kdy zjistíme, že příčinou zamýšleného odchodu pracovníků je nedůvěra ve vedení, která snížila pracovní morálku týmu. Bylo by tedy možné odchod pracovníků předvídat na základě zjišťování jejich postojů vůči vedení, což by představovalo latentní proměnnou. Bylo by ale také možné predikovat odchod pracovníků na základě morálky týmu, kdy postoj k vedení a odchod pracovníků mohou vystupovat jako navzájem nezávislé proměnné.[2]
V síťových modelech jsou manifestní proměnné označovány jako uzly („nodes“) a vztahy mezi nimi jsou označovány jako hrany („edges“). Nejčastěji jsou přitom užívány „undirected network models“, kde není vyjádřen směr kauzality vztahu mezi proměnnými, jelikož je předpoklad, že se proměnné mohou ovlivňovat navzájem obousměrně. Graficky síla spojnic mezi uzly znázorňuje sílu vztahu mezi proměnnými. Některé proměnné přitom mají vzájemně silnější asociace než jiné, takže vytvářejí clustery, ve kterých je větší pravděpodobnost společné aktivace. Například nespavost má silnou asociaci s únavou, ale slabší asociaci s pocity viny, které jsou pravděpodobně mediovány např. problémem se soustředěním. Pokud je tedy aktivován symptom nespavosti, velmi pravděpodobně bude také přítomen symptom únavy, ale již s menší pravděpodobností pocity viny.[3]
Síťové modely se uplatňují v aktuálně se rozvíjejícím přístupu k psychopatologii a klasifikaci psychiatrických diagnóz a ve vysvětlení výskytu komorbidit.[4] Symptomy z hlediska tohoto přístupu nejsou považovány pouze za pasivní indikátory určité latentní nemoci, ale jsou to primární jednotky, které tvoří síť a přímo souvisí s dalšími symptomy, s nimiž se vzájemně ovlivňují a udržují. Zároveň může být síť symptomů aktivována také vnějším činitelem (např. ztráta partnera aktivuje depresivní náladu). Některé symptomy jsou společné více onemocněním a fungují jako tzv. „bridge symptoms“, což znamená, že mohou aktivovat sítě dalších symptomů a tedy vést k současnému výskytu dalšího onemocnění.[5] Přestože dané symptomy mají nejsilnější asociace se svou vlastní sítí symptomů, dochází zde ke strukturálnímu překryvu některých nemocí a tedy ke vzniku komorbidit. Klasifikace diagnózy pak v rámci síťových modelů představuje označení daného systému symptomů, nikoli latentní proměnnou, která způsobuje dané symptomy nebo je jejich výsledkem. Diagnóza je popisem určité specifické sítě symptomů, které mají silné spoje a vzájemně se udržují v aktivaci i dlouhou dobu po odeznění spouštěče.[3] Jsou vytvářeny také síťové modely samotných klasifikací nemocí a diagnostických manuálů.[6][7]
Duševní zdraví je pak možné z hlediska síťových modelů popsat jako stav rovnováhy, do které se systém vrací, pokud je narušen. Duševní nemoc je z tohoto hlediska stabilní stav silně propojené sítě symptomů, které se vzájemně udržují v aktivaci. Resilience je pak dispozice slabě propojených sítí rychle se vracet do stabilního stavu mentálního zdraví, kdežto vulnerabilita je dispozice silně propojených sítí udržovat se ve stavu aktivace po zapůsobení spouštěče. Klinik v rámci diagnostiky a léčby zjišťuje, jaké symptomy jsou aktivovány a jakými interakcemi v síti symptomů se udržují, což je částečně již přirozeně obsaženo v klasifikaci DSM-5. V rámci intervencí je pak možné ovlivnit jeden nebo více symptomů, odstranit jeden nebo více spouštěčů, nebo změnit strukturu sítě symptomů a jejich spojů.[3]
Praktické aplikace síťových modelů v klinické psychologii můžeme kromě modelu komorbidity nalézt např. v modelu deprese[8], úzkostné poruchy[9], PTSD[10], autismu[11], psychotických poruch[12] či látkových závislostí[13]. Mimo klinickou psychologii se můžeme setkat se síťovými modely např. pro teorii inteligence[14], attachmentu[15] či osobnostních rysů[16].
Kauzální analýza
Teorie síťových modelů je užívaná také ve statistických procedurách, konkrétně v kauzální analýze. Tato technika umožňuje odhadovat kauzalitu na základě observačních studií, bez nutnosti provádění randomizovaného kontrolovaného experimentu. Díky kauzálním modelům je tedy možné testovat i hypotézy, které by jinak z etických či praktických důvodů nemohly být testovány.
Kauzálnímu modelování se věnoval počítačový vědec a filosof Judea Pearl. Ten popisuje tři úrovně kauzálních modelů: asociace (pozorování), intervence (dělání) a kontrafaktualita (představování). Na úrovni asociací pozorujeme v proměnných vzorce, které můžeme vyjádřit jako korelace. Zde nemůžeme vyslovit žádný předpoklad ohledně kauzality v datech. Na úrovni intervence už predikujeme kauzální vztahy mezi proměnnými na základě experimentální intervence, případně na základě odhadu z observačních dat.
Nejvyšší úroveň je pak úroveň kontrafaktuality, kde zvažujeme a konstruujeme alternativní scénář, co by se s proměnnou stalo za jiných podmínek. Na této úrovni je tak možné pravděpodobnostně popsat možné chování objektů bez nutnosti provádět experimentální intervenci. Je zde vyjádřen vztah „Y by bylo y, když X by bylo x v situaci U = u“, tedy Yx(u) = y. Model, který dokáže popsat i kontrafaktuality, umožňuje přesné intervence s predikcí jejich dopadů a nejlépe tak vyjadřuje kauzální vztahy mezi proměnnými. Příkladem těchto modelů jsou fyzikální zákony, které popisují chování objektů za různých okolností (např. setrvačnost, která popisuje, že když na objekt nepůsobí síla, objekt nemění směr ani rychlost pohybu).[17][18]
Jako statistická technika pro testování a odhadování kauzálních modelů se užívá strukturní modelování (anglicky Structural equation modeling, SEM), konkrétně např. konfirmační faktorová analýza nebo pěšinková („path“) analýza.[18]
Adaptivní testování
Dalším trendem v psychometrii je adaptivní testování. Tento způsob testování umožňuje přizpůsobit test flexibilně výkonu konkrétního člověka tak, aby absolvoval jen ty položky, které umožní co nejpřesnější odhad jeho schopností. Testovaný člověk tak nemusí procházet všechny položky, z nichž určitá část by byla výrazně nad nebo pod jeho schopnosti. Díky tomu je test kratší, účastník není unaven příliš jednoduchými položkami ani stresován příliš obtížnými položkami. Test může být zastaven po dosažení délky testu, doby testu, stanovené přesnosti kritéria na odhad schopnosti (např. směrodatná chyba o velikosti 0.5) nebo na základě stanoveného klasifikačního kritéria (např. prošel/neprošel, když je konfidenční interval nad hranicí stanoveného cut-off skóru).
Adaptivní test na základě odpovědí opakovaně vypočítává predikce následujících odpovědí a přizpůsobuje tomu obtížnost položek. Tento způsob testování byl umožněn až v posledních letech díky rozvoji počítačové techniky, jelikož jsou potřeba rychlé výpočty v průběhu testování. Jedním z přístupů, na základě kterého tento typ testování funguje, je Item response theory (IRT), neboli teorie odpovědi na položku. Tento přístup je alternativou ke klasickému testovému přístupu. Liší se tím, že k testu přistupuje jako k souboru samostatně fungujících položek, o jejichž fungování můžeme získat informace jako např. informativnost jednotlivých položek či jejich obtížnost. Díky tomu pak adaptivní test může přizpůsobovat obtížnost položek aktuálnímu výkonu testovaného. (poznámky z předmětu Vybraná témata z psychometrie)
Metaanalýzy
V současnosti je v psychologii kladen důraz na vytváření a využívání metaanalýz. Jde o nejvyšší úroveň poznání v hierarchii evidence. Hlavním přínosem metaanalýzy je možnost dát dohromady větší množství jednotlivých studií týkajících se určitého tématu a kvantifikovat souhrnně jejich výsledky. Jednotlivé výsledky jsou statisticky syntetizovány do jednoho pomocí vypočítání váženého průměru velikostí účinku zahrnutých studií. Díky tomu je možné dospět k přesnějšímu odhadu skutečného efektu než z jednotlivých studií.
Při tvorbě metaanalýzy je nejprve definována výzkumná otázka, kterou chtějí výzkumníci analyzovat. Následuje proces vyhledávání a selekce studií, který by měl být v metaanalýze podrobně zaznamenán. K tomu se nejčastěji využívá PRISMA diagram, kam se zaznamenávají jednotlivé kroky a počet vyloučených a ponechaných studií v každém kroku, případně další podrobnosti. Zaznamenávají se také klíčová slova a databáze, kde byly studie vyhledávány. Zároveň je důležité stanovit si a popsat výběrová kritéria, podle kterých budou studie do metaanalýzy zahrnuty (např. minimální počet participantů, věk, použité metody atd.), aby byla zajištěna kvalita a také určitá srovnatelnost studií. Vybrané studie se pak dále kódují podle velikostí účinku a standardní chyby, případně je možné kódovat i další informace a analyzovat také podskupiny studií. (poznámky z předmětu Metodologická praktika v psychologii)
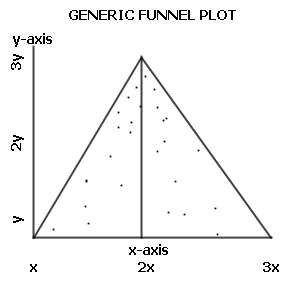
Ve výsledcích metaanalýzy pak většinou nalezneme forest plot, což je graf znázorňující velikosti efektu jednotlivých studií a celkovou průměrnou velikost efektu s konfidenčními intervaly. Metaanalýza totiž pracuje také se standardní chybou jednotlivých studií a zohledňuje tak i jejich různou přesnost. Studie by se měly nacházet normálně rozdělené kolem skutečné hodnoty. To je možné zobrazit v tzv. funnel plotu, na základě kterého je možné posoudit případné zkreslení (studie s vyšší přesností by se měly nacházet blíže k průměrné velikosti účinku). (poznámky z předmětu Metodologická praktika v psychologii)
Výčet údajů, které je potřeba v metaanalýze pro transparentnost uvést, je popsán v PRISMA (Preferred Reporting Items for Systematic reviews and Meta-Analyses) modelu. Tento model obsahující 27 otázek a čtyřstupňový diagram výzkumníci vytvořili pro zvýšení kvality reportování metaanalýz a review.[19]
Výsledky metaanalýzy mohou být ale také zkreslené. Jedním z hlavních důvodů je publikační zkreslení, kdy jsou publikovány pouze studie, které dospěly k nějakému signifikantnímu výsledku. Do metaanalýzy se pak často nedostanou studie, které daný efekt nepotvrdily, a výsledek tak nadhodnocuje skutečnou hodnotu. Existují metody, jak toto zkreslení identifikovat (např. Cochrane Risk of Bias Tool) a také korekční metody (např. p-curve, p-uniform). Více o těchto metodách je možné nalézt v citovaných článcích[20][21]. Dalším problémem může být přílišná různorodost studií. Pokud studie nejsou srovnatelné (např. v designu, věku participantů a dalších důležitých proměnných pro danou oblast), tak neodhadujeme jeden efekt, ale spíše distribuci efektů související s těmito faktory. Je proto důležité stanovit si kritéria výběru studií a zajistit homogenitu v důležitých proměnných. Zkreslující může být také výběr studií, jelikož výzkumníci mají u metaanalýzy velkou flexibilitu v tom, jaké studie do ní zařadí. Nakonec pokud vycházíme z více metaanalýz, je potřeba se podívat, zda není velký překryv mezi jejich zařazenými studiemi. Pokud by bylo vysoké procento studií společné, nemohli bychom s těmito metaanalýzami pracovat jako s nezávislými důkazy o výsledném efektu. (poznámky z předmětu Metodologická praktika v psychologii)
Bayesovská statistika
Dalším rozvíjejícím se trendem nejen v psychologii je užívání Bayesovského přístupu ke statistickým analýzám. Je to alternativa frekventistického přístupu, kde pravděpodobnost je chápána jako relativní četnost jevu v nekonečném počtu opakování. Bayesiánský přístup interpretuje pravděpodobnost jako stupeň přesvědčení o výskytu daného jevu. Vychází z toho, že pravděpodobnost existuje pouze v mysli lidí a je tedy subjektivní. Stupeň přesvědčení může být založen na předchozích znalostech o jevu, jako jsou např. předchozí výsledky experimentů. Výchozí hypotéza je pak dále zpřesňována na základě nově získaných informací a zkušeností. (poznámky z Kognitivní psychologie)
Matematicky je v tomto přístupu využíván Bayesův teorém, který pracuje s podmíněnými pravděpodobnostmi: P(A|B) = [P(B|A)P(A)]/P(B). Předmětem výpočtu zde tedy není pouze pravděpodobnost jevu A, ale pravděpodobnost jevu A při splnění určité podmínky, při současné platnosti jevu B. Jinými slovy zjišťujeme, jaká je pravděpodobnost platnosti hypotézy, pokud pozorujeme určitá data. Díky tomu také můžeme zpřesňovat apriorní očekávání (hypotéza, P(A)) na základě nových důkazů či dat, která do výpočtu zahrneme.[22]
Apriorní pravděpodobnost (P(A)) je daná naší subjektivní zkušeností či teoretickou znalostí, co víme bez ohledu na existující data, je to očekávaná pravděpodobnost výskytu nějakého jevu před provedením testu. Pokud žádné informace k dispozici nemáme, přisuzujeme všem hypotézám stejnou pravděpodobnost a teprve po získání dalších informací (např. provedení testu) můžeme odhad pravděpodobnosti zpřesňovat. Do výpočtu je pak zahrnuta kromě pravděpodobnosti nastání jednotlivých jevů A a B také opačná podmíněná pravděpodobnost, tedy pravděpodobnost nastání jevu B za platnosti jevu A (P(B|A)), nebo-li „věrohodnostní funkce“. Jde o pravděpodobnost výskytu pozorovaných dat za předpokladu platnosti hypotézy.[22]
Aposteriorní pravděpodobnost (P(A|B)) tedy počítáme jako apriorní pravděpodobnost (P(A)) vynásobenou věrohodnostním poměrem (P(B|A)/P(B)). Bayesovský přístup tak klade důraz na to, jak se pravděpodobnostní očekávání mění na základě nových důkazů a jak je možné zpřesňovat původní hypotézy na základě nových dat. Statistické metody v Bayesovském přístupu pak vycházejí z tohoto pravidla.[22]
Jako příklad využití Bayesova teorému použijeme otázku, jaká je pravděpodobnost, že má určitý člověk spalničky. Na základě literatury máme apriorní předpoklad, že v populaci má spalničky 1 % lidí daného věku. Test, který použijeme, je reliabilní na 99 %, takže 99 nemocných lidí ze 100 vyjde v testu jako pozitivní, 99 zdravých lidí ze 100 vyjde jako negativní. Chceme zjistit, jaká je pravděpodobnost, že když nám vyjde pozitivní test, tak máme opravdu spalničky, tedy P(H|E). Díky Bayesovu teorému můžeme zjistit, že první intuitivní odhad je často mylný, jelikož lidé mají tendenci zanedbávat celkovou pravděpodobnost jevu v populaci. Když užijeme Bayesovu větu, tak naše apriorní hypotéza P(H) je 0.01 (předpoklad, že 1 % lidí v populaci má spalničky). Pravděpodobnost pozitivního testu při spalničkách, neboli spolehlivost testu P(E|H) je 0.99. Dopočítat potřebujeme ještě P(E), tedy pravděpodobnost toho, že nám vyjde pozitivní test, bez ohledu na to, jaká je realita. Potřebujeme totiž zohlednit i situaci, kdy vyjde test falešně pozitivní, tedy v situaci, kdy ve skutečnosti spalničky nemáme. P(E) tedy zahrnuje pravděpodobnost skutečně pozitivních i falešně pozitivních výsledků testu. Pravděpodobnost falešně pozitivních spočítáme jako falešnou pozitivitu v testu vynásobenou počtem lidí, kteří nejsou nemocní, tedy 0.01 * 0.99 = 0.0099 (0.01 představuje doplněk do 0.99, což je 99 % zdravých, co vyjdou negativně; 0.99 je doplněk do 0.01, což je 1 % nemocných v populaci). Pravděpodobnost skutečně pozitivního výsledku je pak pravděpodobnost toho, že má člověk spalničky vynásobená pravděpodobností toho, že má spalničky a zároveň pozitivní test, neboli P(H) * P(E|H), takže 0.01 * 0.99 = 0.0099. Pravděpodobnost pozitivního testu je tedy P(E) = 0.0099 + 0.0099 = 0.0198. Když všechny tyto informace dosadíme do Bayesova vzorce, získáme P(H|E) = [P(E|H)P(H)]/P(E), tedy P(H|E) = (0.99 * 0.01)/0.0198 = 0.5 (pravděpodobnost spalniček při pozitivním testu = pravděpodobnost reálně pozitivního testu děleno pravděpodobnost všech pozitivních testů). Získáme tedy výsledek, že pravděpodobnost, že máme skutečně spalničky, když nám vyjde pozitivní test, je 50 %. Když je pak člověk testován znovu a znovu aplikujeme Bayesovu větu, dojde ke snížení míry neurčitosti, jelikož máme přesnější vstup z předchozího testování, tedy P(H) = 0.5 (místo původního teoretického předpokladu 1 % z populace). Pokud by i druhý test vyšel pozitivně, pravděpodobnost skutečné přítomnosti nemoci by už vyšla 99 %. Další test by pak odhad dále zpřesnil. (poznámky z Kognitivní psychologie)
V závěrech výzkumů s využitím Bayesiánského přístupu se pak místo prosté posteriorní pravděpodobnosti nulové a alternativní hypotézy za platnosti dat P(H0|E) a P(H1|E) většinou uvádí tzv. Bayesův faktor P(E|H1)/P(E|H0). Ten zastupuje podobnou roli jako p-hodnota v klasickém přístupu k testování hypotéz a vyjadřuje sílu evidence poskytnutou daty. Bayesův faktor větší než 1 podporuje alternativní hypotézu, přičemž za pozitivní evidenci se většinou považuje faktor 3–20 a za silnou evidenci se považuje faktor 20–150. Důvod, proč se nereportuje posteriorní poměr P(H1|E)/P(H0|E) vyjadřující relativní pravděpodobnost nulové a alternativní hypotézy po získání dat je, že různí výzkumníci mají různá apriorní očekávání. Když si tedy Bayesovým faktorem vynásobí svá vlastní apriorní očekávání, získají vlastní posteriorní poměr.[22]
Budování psychologických teorií
Dalším důležitým aktuálním tématem v psychologii je budování teorií. V posledních letech byl kladen důraz na zlepšení statistických a metodologických postupů v psychologickém výzkumu, aby se zvýšila reliabilita a replikabilita výsledků a aby se mimo jiné předešlo pochybným výzkumným praktikám jako např. p-hacking nebo cherry picking. K řešení těchto otázek napomohl větší důraz na otevřenost vědy a postupy jako předregistrace výzkumu nebo sdílení dat a kódu.[23]
Mnoho výzkumníků[24][25][26] však v současnosti upozorňuje na to, že v psychologii je hlubší problém, kterým je krize teorie. Je mnoho psychologických fenoménů a výsledků výzkumů, které vyžadují vysvětlení, ovšem málo teorií, které by je vysvětlovaly. Výzkumníci například často považují statistický model za teoretický model – jako závěr svého výzkumu například uvedou, že určitý model je vysvětlitelný latentní proměnnou. To je statisticky možné vždy, důležité ale je, co to znamená teoreticky, zda daný konstrukt v psychologii existuje. Nelze tedy zaměňovat statistický model za teoretický. Teorie v psychologii jsou také většinou slabé, jelikož v nich často zůstává mnoho neznámých předpokladů či moderujících proměnných, nedokážou přesně predikovat, za jakých podmínek může být daný efekt pozorován. Je tedy obtížné tyto teorie používat k vysvětlení či predikci jevů. Silné teorie oproti tomu předkládají jasné vysvětlení fenoménu, ne pouze popis dat, a jsou většinou prezentovány pomocí formálního matematického modelu. Díky těmto teoriím je možné predikovat i scénáře, které ve skutečnosti nenastaly.[27]
Jedním z možných přístupů pro vytváření silnějších teorií v psychologii je formalizování teorie do matematického modelu, kde jsou jasně vyjádřené všechny předpoklady a podmínky. Ten umožňuje simulovat data, jak by vypadala, pokud by byla teorie platná, což je následně možné srovnat se statistickým modelem reálných získaných dat. Rozdíly mezi těmito modely pak mohou vést k úpravě teorie. Práce s formálními modely také umožňuje lepší přístupnost testování teorií jinými výzkumníky, než verbální teorie, kde se replikující výzkumníci nejdříve musí s těmi původními domluvit na tom, jaké jsou podmínky, předpoklady a omezení dané teorie.[27] V současnosti někteří výzkumníci přicházejí s modely či návody, jak metodologicky postupovat při budování teorií v psychologii[24].
Externí nepublikované zdroje
Ke zpracování článku byly uplatněny také poznámky z přednášek RNDr. Patrície Martinkové, Ph.D. získané v rámci kurzu Vybraná témata z psychometrie (nyní pod názvem Statistické metody v psychometrii) vyučovaného na Katedře pravděpodobnosti a matematické statistiky MFF UK. Dále byly využity poznámky z přednášky o metaanalýzách Mgr. Ing. Marka Vranky v rámci předmětu Metodologická praktika v psychologii vyučovaného na Katedře psychologie (KPS) FF UK. Také byly využity poznámky z přednášek RNDr. Terezy Nekovářové, Ph.D. o Bayesiánské teorii v rámci předmětu Kognitivní psychologie vyučovaném na KPS FF UK.
Odkazy
Reference
- ↑ 1,0 1,1 1,2 Schmittmann, V. D., Cramer, A. O. J., Waldorp, L. J., Epskamp, S., Kievit, R. A., & Borsboom, D. (2013). Deconstructing the construct: A network perspective on psychological phenomena. New Ideas in Psychology, 31(1). doi:10.1016/j.newideapsych.2011.02.007
- ↑ Predictive Psychometrics (n.d.). Network psychometrics. https://predictivepsychometrics.com/network-psychometrics/?fbclid=IwAR08j8YwUYbaHvN3KqluXDt5XYH93vTIUkyNnl08aoc02od2z9lrpCPPriU
- ↑ 3,0 3,1 3,2 Borsboom, D. (2017). A network theory of mental disorders. World of Psychiatry 16(1), 5–13. doi: 10.1002/wps.20375
- ↑ Borsboom, D., Cramer, A. O. J., Schmittmann, V. D., Epskamp, S., & Waldorp, L. J. (2011). The small world of psychopathology. PLoS One 6(11), e27407. https://doi.org/10.1371/journal.pone.0027407
- ↑ Cramer, A. O. J., Waldorp, L. J., Van der Maas, H. L. J., & Borsboom, D. (2010). Comorbidity: A network perspective. Behavioral and BrainSciences 33, 137–193. doi: 10.1017/S0140525X09991567
- ↑ Goekoop, R., & Goekoop, J. G. (2014). A network view on psychiatric disorders: Network clusters of symptoms as elementary syndromes of psychopathology. PLoS One 9(11), e112734. https://doi.org/10.1371/journal.pone.0112734
- ↑ Boschloo, L., van Borkulo, C. D., Rhemtulla, M., Keyes, K. M., Borsboom, D., & Schoevers, R. A. (2015). The network structure of symptoms of the Diagnostic and Statistical Manual of Mental Disorders. PLoS One 10(9), e0137621. https://doi.org/10.1371/journal.pone.0137621
- ↑ Fried, E. I., Epskamp, S., Nesse, R. M., Tuerlinckx, F., & Borsboom, D. (2016). What are ‘good’ depression symptoms? Comparing the centrality of DSM and non-DSM symptoms of depression in a network analysis. Journal of Affective Disorders 189, 314–320. DOI: 10.1016/j.jad.2015.09.005
- ↑ Heeren, A., & McNally, R. J. (2016). An integrative network approach to Social Anxiety Disorder: the complex dynamic interplay among attentional bias for threat, attentional control, and symptoms. Journal of Anxiety Disorders 42, 95–104. DOI: 10.1016/j.janxdis.2016.06.009
- ↑ McNally, R. J., Robinaugh, D. J., Wu, G. W. Y., Wang, L., Deserno, M. K., & Borsboom, D. (2014). Mental disorders as causal systems: A network approach to Posttraumatic Stress Disorder. Clinical Psychological Science 3(6), 836–49. https://doi.org/10.1177/2167702614553230
- ↑ Ruzzano, L., Borsboom, D., & Geurts, H. M. (2014). Repetitive behaviors in autism and obsessive-compulsive disorder: New perspectives from a network analysis. Journal of Autism and Developmental Disorders 45, 192–202. DOI: 10.1007/s10803-014-2204-9
- ↑ Bak, M., Drukker, M., Hasmi, L., & van Os, J. (2016). An n=1 clinical network analysis of symptoms and treatment in psychosis. PLoS One 11(10), e0165762. https://doi.org/10.1371/journal.pone.0162811
- ↑ Rhemtulla, M., Fried, E. I., Aggen, S. H., Tuerlinckx, F., Kendler, K. S., & Borsboom, D. (2016). Network analysis of substance abuse and dependence symptoms. Drug and Alcohol Dependence 161, 230–237. doi: 10.1016/j.drugalcdep.2016.02.005
- ↑ Van der Maas, H. L. J., Dolan, C., Grasman, R. P. P. P., Wicherts, J. M., Huizenga, H. M., & Raijmakers, M. E. J. (2006). A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review 113(4), 842–861. https://doi.org/10.1037/0033-295X.113.4.842
- ↑ Hermans, A., Muhammad, S., Treur, J. (2021). An Adaptive Network Model of Attachment Theory. In: Paszynski, M., Kranzlmüller, D., Krzhizhanovskaya, V. V., Dongarra, J. J., Sloot, P. M. (eds) Computational Science – ICCS 2021. ICCS 2021. Lecture Notes in Computer Science, Springer 12744. https://doi.org/10.1007/978-3-030-77967-2_39
- ↑ Cramer, A. O. J., van der Sluis, S., Noordhof, A., Wichers, M., Geschwind, N., Aggen, S. H., Kendler, K. S., & Borsboom, D. (2012). Dimensions of normal personality as networks in search of equilibrium: You can't like parties if you don't like people. European Journal of Personality 26(4), 414–31. https://doi.org/10.1002/per.1866
- ↑ Pearl, J. (2019). Causal and Counterfactual Inference. In M. Knauff, & W. Spohn (Eds.), The Handbook of Rationality, Section 7.1, pp. 427–438, The MIT Press. https://ftp.cs.ucla.edu/pub/stat_ser/r485.pdf
- ↑ 18,0 18,1 Pearl, J. (2009). Causal inference in statistics: An overview. Statistics Survey 3, 96–146. DOI: 10.1214/09-SS057
- ↑ Liberati, A., Altman, D. G., Tetzlaff, J., Mulrow, C., Gøtzsche, P. C., Ioannidis, J. P. A., Clarke, M., Devereaux, P. J., Kleijnen, J., & Moher, D. (2009). The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: Explanation and elaboration. Journal of Clinical Epidemiology 10(62), e1–e34. DOI: 10.1016/j.jclinepi.2009.06.006
- ↑ Carter, E. C., Schönbrodt, F. D., Gervais, W. M., & Hilgard, J. (2019). Correcting for bias in psychology: A comparison of meta-analytic methods. Advances in Methods and Practices in Psychological Science 2, 115–144. https://doi.org/10.1177/2515245919847196
- ↑ Page, M. J., McKenzie, J. E., & Higgins, J. P. T. (2018). Tools for assessing risk of reporting biases in studies and syntheses of studies: A systematic review. BMJ Open 3(8), e019703. DOI: 10.1136/bmjopen-2017-019703
- ↑ 22,0 22,1 22,2 22,3 Navarro, D. J., & Foxcroft, D. R. (2019). Learning statistics with jamovi: a tutorial for psychology students and other beginners. (Version 0.70). DOI: 10.24384/hgc3-7p15 [Available from url: http://learnstatswithjamovi.com]
- ↑ Klein, O., Hardwicke, T. E., Aust, F., Breuer, J., Danielsson, H., Mohr, A. H., Ijzerman, H., Nilsonne, G., Vanpaemel, W., & Frank, M. (2018). A Practical Guide for Transparency in Psychological Science. Collabra: Psychology 4(1), 1–15. 10.1525/collabra.158.
- ↑ 24,0 24,1 Borsboom, D., van der Maas, H. L. J., Dalege, J., Kievit, R., & Haig, B. (2021). Theory construction methodology: A practical framework for theory formation in psychology. Perspectives on Psychological Science 16(4), 756–766. https://doi.org/10.1177/1745691620969647
- ↑ Haslbeck, J., Ryan, O., Robinaugh, D., & Waldorp, L. (2019). Modeling psychopathology: From data models to formal theories. 1–29. Retrieved from https://psyarxiv.com/jgm7f/.
- ↑ Vaidyanathan, U., Vrieze, S. I., & Iacono, W. G. (2015). The power of theory, research design, and transdisciplinary integration in moving psychopathology forward. Psychological Inquiry, 26(3), 209–230.
- ↑ 27,0 27,1 Fried, E. I. (2020). Lack of theory building and testing impedes progress in the factor and network literature. Psychological Inquiry 31(4), 271–288. https://doi.org/10.1080/1047840X.2020.1853461
Další doporučená literatura
Halpern, J. Y. (2019). Actual causality. MIT Press.
Hendl, J. (2004). Přehled statistických metod zpracování dat : analýza a metaanalýza dat. Portál.
Pearl, J. (2009). Causality: Models, reasoning and inference. Cambridge University Press.
Pearl, J., & Mackenzie, D. (2018). The Book of Why: The New Science of Cause and Effect. Basic Books.
Siddaway, A. P., Wood, A. M., & Hedges, L. V. (2019). How to Do a Systematic Review: A Best Practice Guide for Conducting and Reporting Narrative Reviews, Meta-Analyses, and Meta-Syntheses. Annual Review of Psychology 1(70), 747–770. DOI: 10.1146/annurev-psych-010418-102803
Zdroje obrázků
Ilustrativní obrázek modelu, Mckinseyho 7S: Soubor:Mckinsey-7s-model-template.png#file
Ilustrativní forest plot: James Grellier, https://commons.wikimedia.org/wiki/File:Generic_forest_plot.png
Ilustrativní funnel plot neprokazující zkreslení: https://commons.wikimedia.org/wiki/File:Funnelplot.png
Bayesův teorém: https://commons.wikimedia.org/wiki/File:Bayes%27_Theorem_MMB_01.jpg
Externí odkazy
https://link.springer.com/article/10.1007/s12144-021-01957-4 – seznam literatury k různým otázkám provádění metaanalýz
https://prisma-statement.org/ – PRISMA model pro reportování metaanalýz
https://www.riskofbias.info/ – nástroj pro odhalování zkreslení metaanalýz
http://www.cebm.brown.edu/openmeta/ – nástroj pro tvorbu metaanalýz
https://osf.io/uscfx – seznam literatury pro seznámení se s budováním teorií v psychologii (zdroj: Fried, E. I. (2020). Lack of Theory Building and Testing Impedes Progress in The Factor and Network Literature. Psychological Inquiry 31(4), 271–288. https://doi.org/10.1080/1047840X.2020.1853461)
https://www.youtube.com/watch?v=Zxm4Xxvzohk - YouTube video z kanálu Art of the Problem: Conditional probability explained visually (Bayes' Theorem)
https://web.archive.org/web/20070613184853/http://yudkowsky.net/bayes/bayes.html - Yudkowsky, E. (2003). Intuitive Explanation of Bayesian Reasoning.
Odkazy na související články
Replikační krize v psychologii
Alternativní přístupy k psychodiagnostice v pedagogické a školní psychologii
Sekundární analýza dat a metaanalýza
Klíčová slova
psychometrie, psychologická metodologie, síťové modely