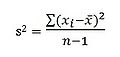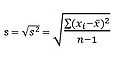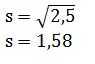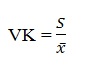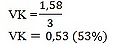Míry variability: Porovnání verzí
| Řádek 60: | Řádek 60: | ||
</gallery> | </gallery> | ||
| − | == | + | == Zdroje == |
Ferjenčík, J. (2006). Základy štatistických metód v sociálnych vedách. Košice: Univerzita Pavla Jozefa Šafárika. | Ferjenčík, J. (2006). Základy štatistických metód v sociálnych vedách. Košice: Univerzita Pavla Jozefa Šafárika. | ||
<br /> | <br /> | ||
| Řádek 66: | Řádek 66: | ||
<br /> | <br /> | ||
Zvára, K. (2004). Biostatistika. Praha: Nakladatelství Karolinum. | Zvára, K. (2004). Biostatistika. Praha: Nakladatelství Karolinum. | ||
| + | [[Kategorie: Statistika|*]] | ||
Verze z 14. 4. 2014, 08:34
Pokud chceme charakterizovat náhodně proměnlivé údaje v určitém souboru, nestačí charakterizovat jen střední hodnotu, ale je vhodné určit i míru, v jaké jsou jednotlivé údaje od sebe navzájem rozptýlené. To vymezují míry variability, mezi které se řadí variační rozpětí, rozptyl, směrodatná odchylka a variační koeficient (Hendl, 2006).
Variační rozpětí (Range)
Variační rozpětí je definováno jako rozdíl mezi nejnižší a nejvyšší hodnotou daného souboru a podává informace o tom, v jaké šířce jsou dané údaje rozprostřené na příslušné škále. Označení pro variační rozpětí je R.
R = Xmax - Xmin*
- *U diskrétních proměnných někteří autoři preferují pro výpočet R = (Xmax - Xmin) + 1.
Nevýhodou variačního rozpětí je velká citlivost vůči extrémním hodnotám a také nereflektování způsobu, jakým jsou údaje rozložené uvnitř souboru (Ferjenčík, 2006).
Modelový příklad: {1,2,3,4,5}
R = 5 – 1
R = 4
Rozptyl
Rozptyl je definován jako průměrná kvadratická odchylka mezi údaji souboru a jejich aritmetickým průměrem (Ferjenčík, 2006).
Podle Hendla (2006) není při větších rozsazích významný rozdíl mezi číslem n nebo n – 1. Dělení číslem n se používá v případě, kdy počítáme rozptyl pro všechny prvky populace.
Modelový příklad: {1,2,3,4,5}
Interpretace rozptylu může být někdy nesrozumitelná, a proto se v praxi jako nejčastější ukazovatel míry variability používá druhá odmocnina z rozptylu označovaná jako směrodatná odchylka (Ferjenčík, 2006).
Směrodatná odchylka
Směrodatná odchylka je průměrná vzdálenost mezi jednotlivými údaji a jejich aritmetickým průměrem. Informuje nás o tom, jak daleko jsou v průměru jednotlivé údaje rozprostřené kolem svého aritmetického průměru (Ferjenčík, 2006). Vypočítá se jako odmocnina z rozptylu a na rozdíl od rozptylu má stejný fyzikální rozměr jako původní veličina (Zvára, 2004).
Modelový příklad: {1,2,3,4,5}
Variační koeficient
Variační koeficient se používá v případě, kdy chceme posoudit relativní velikost rozptýlenosti dat vzhledem k průměru a někdy se uvádí v procentech (Hendl, 2006). Slouží k porovnání variability souborů, které mají nestejné průměry (Zvára, 2004).
Modelový příklad: {1,2,3,4,5}
Zdroje
Ferjenčík, J. (2006). Základy štatistických metód v sociálnych vedách. Košice: Univerzita Pavla Jozefa Šafárika.
Hendl, J. (2006). Přehled statistických metod zpracování dat. Praha: Portál.
Zvára, K. (2004). Biostatistika. Praha: Nakladatelství Karolinum.