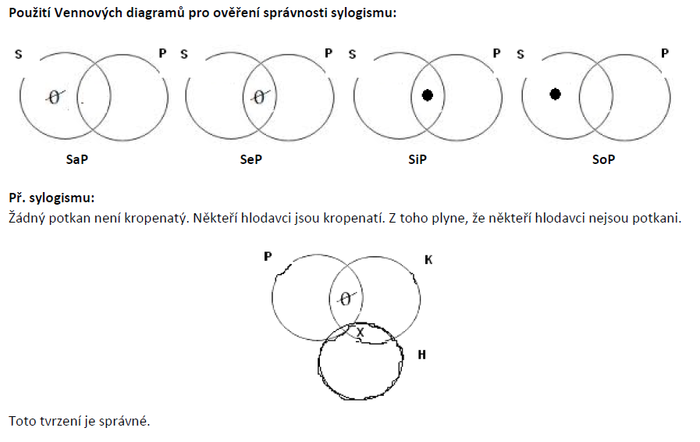
Popište pojem sylogismu a uveďte, jakým způsobem lze použít Vennovy diagramy pro ověření správnosti sylogismu: Porovnání verzí
| Řádek 19: | Řádek 19: | ||
* '''SaP''': Obecný kladný výrok | * '''SaP''': Obecný kladný výrok | ||
- Všechna S jsou P = ∀x [S(x) → P(x)] | - Všechna S jsou P = ∀x [S(x) → P(x)] | ||
| − | * '''SeP: Obecný záporný výrok | + | * '''SeP''': Obecný záporný výrok |
- Žádné S není P = ∀x [S(x) → ¬P(x)] | - Žádné S není P = ∀x [S(x) → ¬P(x)] | ||
| + | *'''SiP''': Částečný kladný výrok | ||
- Některé S je P = ∃x [S(x) ∧ P(x)] | - Některé S je P = ∃x [S(x) ∧ P(x)] | ||
* '''SoP''': Částečný záporný výrok | * '''SoP''': Částečný záporný výrok | ||
Verze z 22. 9. 2020, 13:58
Aristotelova logika
Sylogismus – Aristotelův kategorický sylogismus je úsudek, který má právě dvě premisy. Jde o druh logického tvrzení, ve kterém je jeden z výroků (závěr) odvozen z ostatních dvou předpokladů (premis) určité formy.
Dvě premisy a jeden závěr jsou značeny písmeny S, P, M.
| S | P | M |
|---|---|---|
| subjekt | predikát | medián |
- Subjekt S - termín, který stojí v závěru na místě subjektu (ve smyslu predikátové
logiky) a vyskytuje se ve druhé premise
- Predikát P - termín, který stojí v závěru na místě predikátu (ve smyslu predikátové
logiky) a vyskytuje se v první premise
- Střední člen M - vyskytuje se v obou premisách, avšak nikoli v závěru.[1]
- SaP: Obecný kladný výrok
- Všechna S jsou P = ∀x [S(x) → P(x)]
- SeP: Obecný záporný výrok
- Žádné S není P = ∀x [S(x) → ¬P(x)]
- SiP: Částečný kladný výrok
- Některé S je P = ∃x [S(x) ∧ P(x)]
- SoP: Částečný záporný výrok
- Některé S není P = ∃x [S(x) ∧ ¬P(x)]