Šifrování s veřejným klíčem (metoda RSA): Porovnání verzí
| (Není zobrazeno 8 mezilehlých verzí od stejného uživatele.) | |||
| Řádek 1: | Řádek 1: | ||
| − | ''' | + | '''Šifrování veřejným klíčem''' je metoda využívající principy asymetrického šifrování, které se od 70. let v kryptografii používá. Zásluhu na tom mají W. Diffie a M. Hellman, kteří položili základy asymetrického šifrování na základě diskrétního algoritmu. |
| − | K oboru kryptologie neoddělitelně patří pojem ''klíč'', který v tomto případě představuje | + | == Kryptografie == |
| + | '''[[Kryptografie]]''' je nauka o metodách utajování významu přenášených zpráv. Tato nauka je někdy nazývána jako '''šifrování''', jelikož používá tzv. '''šifrování dat''', což je proces, během kterého se nezabezpečená [[data]] převádí na data šifrovaná (zabezpečená), která dokáže dešifrovat jen majitel dešifrovacího klíče. Výsledný nesrozumitelný text, vzniklý pomocí [[Algoritmy kryptologie|šifrovacího algoritmu]] se nazývá '''[[Šifry|šifra]]'''. Kryptografie patří společně s kryptoanalýzou (luštění šifrovaných zpráv) pod obor [[Základní rozdělení kryptologie|kryptologie]]. | ||
| + | |||
| + | K oboru kryptologie neoddělitelně patří [[Základní pojmy v kryptologii|pojem ''klíč'']], který v tomto případě představuje část informace, kterou si strany, které mezi sebou komunikují, vymění nějakým bezpečným kanálem. Klíč upřesňuje, jak se šifra chová. Například pokud abychom šifrovali text pomocí posouvání písmen dle abecedy, tak klíčem pak rozumíme ten počet písmen, o který se posouváme. | ||
<br /> | <br /> | ||
| Řádek 9: | Řádek 12: | ||
* '''soukromý klíč -''' pro dešifrování u asymetrického šifrování | * '''soukromý klíč -''' pro dešifrování u asymetrického šifrování | ||
| − | Důležitá je délka klíče, která je standardně určena počtem bitů. Ovlivňuje časovou náročnost při útoku hrubou silou na danou šifru a tedy bezpečnost šifrovaných dat. Související je síla šifry. Tu stanovují kryptologové, kteří analyzují algoritmy, a hodnotí, jaké úsilí je potřeba k jejich prolomení. | + | Důležitá je délka klíče, která je standardně určena počtem bitů. Ovlivňuje časovou náročnost při útoku hrubou silou na danou šifru, a tedy bezpečnost šifrovaných dat. Související je síla šifry. Tu stanovují kryptologové, kteří analyzují algoritmy, a hodnotí, jaké úsilí je potřeba k jejich prolomení. |
== Symetrické vs. asymetrické šifrování == | == Symetrické vs. asymetrické šifrování == | ||
| − | Pod pojmem '''šifrování''' si | + | Pod pojmem '''šifrování''' je možné si představit takovou [[Komunikace|komunikaci]], kdy si dva nebo více osob posílají tajné zprávy, které lze přečíst jen pomocí zvláštního klíče, který všichni zúčastnění znají a nikdo zvenčí jej nezná (nemůže jej ani uhodnout). Takto funguje [[Symetrická kryptografie|symetrická kryptografie]], která k zašifrování i rozluštění zprávy používá tentýž klíč. Jak si ale účastníci tajný klíč předají? Distribuce klíčů se musí provádět na jiném principu. Šifrování zpráv navíc nemusí mít za cíl pouze udržet nějakou informaci v tajnosti, může také zajišťovat ověření totožnosti osob, např. u [[Digitální podpis|digitálních podpisů]]. Těmto účelům slouží [[Asymetrická kryptografie|asymetrická kryptografie]], ve které se pro zašifrování používá jiný klíč než pro luštění.<ref>[https://is.cuni.cz/webapps/zzp/detail/42950 KREJČOVÁ, Ema. Digitální peníze, 2006]</ref> |
=== Symetrické šifrování === | === Symetrické šifrování === | ||
| − | Princip symetrické metody šifrování zpráv tkví v jednom jediném klíči, který slouží k šifrování i dešifrování zpráv. Tzn. že se '''šifra dešifruje stejným postupem (akorát zpětným) jako byla zašifrována'''. Tento způsob šifrování se objevil již v dobách Julia Caesara, který používal jako princip šifrování posun o 3 písmena v abecedě. Dnes je tato metoda známá jako '''Caesarova šifra''' a je velice jednoduché ji prolomit, jelikož je zde pouze 26 možností (jako je písmen v abecedě, abychom se nedostali zpět na písmenko, které chceme šifrovat). Další symetrická šifra je tzv. '''Polyalfabetická šifra''', která pochází z 15. století, nebo '''Vernamova šifra''' z 19. století, která jako '''první obsahuje princip náhody''', stejně jako kdybychom házeli kostkou a hozená čísla bychom si zapisovali jako seznam náhodných posunů, který by byl následně zaslán protistraně jako společný klíč. Tato šifra se považuje za bezpečnou, jelikož se v ní posuny neopakují, nedají se předvídat a výskyt písmen je rovnoměrný. | + | Princip symetrické metody šifrování zpráv tkví v jednom jediném klíči, který slouží k šifrování i dešifrování zpráv. Tzn. že se '''šifra dešifruje stejným postupem (akorát zpětným) jako byla zašifrována'''. Tento způsob šifrování se objevil již v dobách Julia Caesara, který používal jako princip šifrování posun o 3 písmena v abecedě. Dnes je tato metoda známá jako '''[[Caesarova šifra]]''' a je velice jednoduché ji prolomit, jelikož je zde pouze 26 možností (jako je písmen v abecedě, abychom se nedostali zpět na písmenko, které chceme šifrovat). Další symetrická šifra je tzv. '''Polyalfabetická šifra''', která pochází z 15. století, nebo '''[[Vernamova šifra]]''' z 19. století, která jako '''první obsahuje princip náhody''', stejně jako kdybychom házeli kostkou a hozená čísla bychom si zapisovali jako seznam náhodných posunů, který by byl následně zaslán protistraně jako společný klíč. Tato šifra se považuje za bezpečnou, jelikož se v ní posuny neopakují, nedají se předvídat a výskyt písmen je rovnoměrný. |
=== Asymetrické šifrování === | === Asymetrické šifrování === | ||
| − | Až do 70. let 20. století bylo šifrování založeno na symetrických klíčích. Ovšem postupem času vznikla potřeba komunikovat s více lidmi (např. bankovní účty) a po zavedení internetové sítě také potřeba šifrování dvou stran, které se dohodnou na společném klíči aniž by klíč mohl uniknout jakoukoliv cestou k nějaké třetí nezúčastněné straně. Nad tímto problémem se zamysleli '''W. Diffie a M. Hellman''' v roce 1976 a položili základy asymetrického šifrování s diskrétním algoritmem. V článku ''New Directions in Cryptography'' řešili problém distribuce klíčů a protokol, který v článku popisují se jmenuje [[Diffieho-Helllmanova výměna klíčů]]. Problém diskrétního algoritmu je v tom, že je '''jednoduché zprávu zašifrovat, ale dešifrovat ji zpět je velice náročné, neplatí zde princip dešifrování stejným klíčem''', kterým je zpráva i zašifrována. Metoda, která obsahuje princip asymetrického šifrování se nazývá ''Šifrování s veřejným klíčem''. | + | Až do 70. let 20. století bylo šifrování založeno na symetrických klíčích. Ovšem postupem času vznikla potřeba komunikovat s více lidmi (např. bankovní účty) a po zavedení internetové sítě také potřeba šifrování dvou stran, které se dohodnou na společném klíči, aniž by klíč mohl uniknout jakoukoliv cestou k nějaké třetí nezúčastněné straně. Nad tímto problémem se zamysleli '''W. Diffie a M. Hellman''' v roce 1976 a položili základy asymetrického šifrování s diskrétním algoritmem. V článku ''New Directions in Cryptography'' řešili problém distribuce klíčů a protokol, který v článku popisují se jmenuje [[Diffieho-Helllmanova výměna klíčů]]. Problém diskrétního algoritmu je v tom, že je '''jednoduché zprávu zašifrovat, ale dešifrovat ji zpět je velice náročné, neplatí zde princip dešifrování stejným klíčem''', kterým je zpráva i zašifrována. Metoda, která obsahuje princip asymetrického šifrování se nazývá ''Šifrování s veřejným klíčem''. |
== Šifrování s veřejným klíčem == | == Šifrování s veřejným klíčem == | ||
[[Soubor:Diffie-Hellman Key Exchange (cs).svg|thumb|Diffieho-Hellmanova výměna klíčů znázorněna pomocí míchání barev]] | [[Soubor:Diffie-Hellman Key Exchange (cs).svg|thumb|Diffieho-Hellmanova výměna klíčů znázorněna pomocí míchání barev]] | ||
| − | === Příklad pomocí barev | + | === Příklad pomocí barev === |
| − | Na jedné straně stojí Alice a na druhé Bob. Veřejně se dohodnou na počáteční barvě, např. žluté (tuhle barvu zná tudíž i třetí strana, která chce získat jejich komunikaci). Pak si oba náhodně zvolí svoji vlastní utajenou barvu, kterou přimíchají do žluté. Tím zamaskují jejich soukromé zprávy. Alice si nechá svoji tajnou barvu a směs pošle Bobovi (směs se dostane do rukou třetí strany). Bob si také nechá svojí tajnou barvu a směs pošle Alici (i tato směs se dostane ke třetí straně). Nyní Alice a Bob přidají své soukromé barvy do směsi toho druhého. Vznikne společná tajná barva. Třetí strana nemůže určit barvu, protože k tomu potřebuje jednu ze soukromých barev. Aby se toto dalo udělat s čísly, potřebujeme takovou číselnou operaci, která se dělá snadno v jednom směru, ale obtížně v druhém. | + | Na jedné straně stojí Alice a na druhé Bob. Veřejně se dohodnou na počáteční barvě, např. žluté (tuhle barvu zná tudíž i třetí strana, která chce získat jejich komunikaci). Pak si oba náhodně zvolí svoji vlastní utajenou barvu, kterou přimíchají do žluté. Tím zamaskují jejich soukromé zprávy. Alice si nechá svoji tajnou barvu a směs pošle Bobovi (směs se dostane do rukou třetí strany). Bob si také nechá svojí tajnou barvu a směs pošle Alici (i tato směs se dostane ke třetí straně). Nyní Alice a Bob přidají své soukromé barvy do směsi toho druhého. Vznikne společná tajná barva. Třetí strana nemůže určit barvu, protože k tomu potřebuje jednu ze soukromých barev. Aby se toto dalo udělat s čísly, potřebujeme takovou číselnou operaci, která se dělá snadno v jednom směru, ale obtížně v druhém. <ref>[https://vimeo.com/217214978 MURPHY, Dan, Cryptography in Colors: Public Key Cryptography [přednáška]]</ref> |
=== Příklad s čísli === | === Příklad s čísli === | ||
| − | S barvami to zní jednoduše, pokud chceme šifrování veřejným klíčem pochopit do hloubky, tak si uvedeme i příklad s čísli. Základem šifrování klíčů je '''modulární aritmetika'''. Základní věta aritmetiky je založena na rozkládání čísla na prvočísla, všechna čísla jakkoliv velká se dají rozkládat dokud nenarazíme na prvočíslo. Jinými slovy, všechna čísla se dají vyjádřit několika | + | S barvami to zní jednoduše, pokud chceme šifrování veřejným klíčem pochopit do hloubky, tak si uvedeme i příklad s čísli. Základem šifrování klíčů je '''modulární aritmetika'''. Základní věta aritmetiky je založena na rozkládání čísla na prvočísla, všechna čísla jakkoliv velká se dají rozkládat dokud nenarazíme na prvočíslo. Jinými slovy, všechna čísla se dají vyjádřit několika prvočísly, která představují základní stavební bloky. Alice a Bob se domluví na '''společném klíči, který je prvočíslem (modulus) 17'''. Z čísla 17 máme primitivní kořen (prvočíslo) 3, kterému se říká generátor. Alice si vybere svůj tajný klíč 15 a provede výpočet '''g<sup>x</sup> mod p''' tj. '''3<sup>15</sup> mod 17'''. Výsledkem je číslo 6, které veřejně pošle Bobovi. Bob si vybere také svůj tajný klíč 13 a provede stejný výpočet '''3<sup>13</sup> mod 17'''. Výsledek je 12 a pošle ho veřejně zpět Alici. Alice vezme Bobův veřejný klíč 12 a umocní ho svým tajným číslem ( 12<sup>15</sup> mod 17 = 10 ). Bob udělá to samé s Aliciným veřejným klíčem ( 6<sup>13</sup> mod 17 = 10 ). Oba získávají sdílený tajný klíč. '''Pokud další strana nemá privátní klíče Boba a Alice, tak se k výsledku 10 nijak nedostane''', tato malá čísla byla pouze na ukázku, ale v praxi dešifrovat modulus se stovkami cifer je prakticky nemožné. |
== Digitální podpis == | == Digitální podpis == | ||
| − | Dalším případem užití asymetrického šifrování je ''elektronický / digitální podpis''. Používá se v případě, kdy potřebujeme podepsat důležitý dokument, který by měl nést právě náš podpis a nechceme aby ho kdokoliv během přenosu znehodnotil, manipuloval s ním či někdo podpis zfalšoval. | + | Dalším případem užití asymetrického šifrování je ''elektronický / digitální podpis''. Používá se v případě, kdy potřebujeme podepsat důležitý dokument, který by měl nést právě náš podpis a nechceme, aby ho kdokoliv během přenosu znehodnotil, manipuloval s ním či někdo podpis zfalšoval. Chceme aby si mohl každý ověřit, že jsme podpis opravdu provedli my a nikdo jiný. Provedeme to tedy tak, že zhotovíme hash (otisk zprávy), zašifrujeme ho svým soukromým klíčem a výsledný řetězec přiložíme ke zprávě. Obojí odešleme, každý kdo bude chtít ověřit podpis a autenticitu zprávy může dešifrovat otisk pomocí našeho veřejného klíče a porovnat ho s otiskem příchozí zprávy. Pokud jsou otisky totožné, znamená to, že jsme zprávu psali my a nebylo s ní nijak manipulováno. |
== Metoda RSA == | == Metoda RSA == | ||
| − | |||
| − | V roce 1970 britský matematik a technik James Ellis<ref>James Ellis. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2018-05-01]. Dostupné z: https://en.wikipedia.org/wiki/James_H._Ellis</ref> pracoval s myšlenkou neutajené šifry. Je založena na jednoduchém, a přesto chytrém konceptu. Uzamknutí a odemčení jsou inverzní operace. | + | Jedná se o asymetrickou šifru, která je založena na Eulerově větě, a která je použitelná jak pro šifrování, tak pro podepisování dokumentů. RSA je jedním z '''nejrozšířenějších algoritmů na světě využívající veřejný klíč'''. Každý uživatel internetu používá RSA nebo jeho variantu, aniž by si to uvědomoval. Jeho síla spočívá hlavně v obtížnosti prvočíselného rozpadu. |
| + | |||
| + | === Historie === | ||
| + | V roce 1970 britský matematik a technik '''James Ellis'''<ref>James Ellis. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2018-05-01]. Dostupné z: https://en.wikipedia.org/wiki/James_H._Ellis</ref> pracoval s myšlenkou neutajené šifry. Je založena na jednoduchém, a přesto chytrém konceptu. Uzamknutí a odemčení jsou inverzní operace. Bob by mohl koupit zámek, ponechat si klíč a otevřený zámek poslat Alici. Ona svoji zprávu poté uzamkne a pošle jí zpět majiteli. Vše probíhá bez výměny klíčů. To znamená, že by zámek mohl veřejně nabídnou komukoliv, aby mu díky zámku mohl poslat zprávu. Nicméně James Ellis nikdy nepřišel na matematické řešení. Jeho myšlenka je dále rozdělena na klíče dešifrovací a šifrovací. Dešifrovací klíč provádí inverzní operaci (vrací zpět operaci provedenou šifrovacím klíčem). Řešení nalezl jiný britský matematik '''Clifford Cocks''' v roce 1973.<ref>Clifford Cocks. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2018-05-01]. Dostupné z: https://en.wikipedia.org/wiki/Clifford_Cocks</ref>Objevil ekvivalentní algoritmus k RSA, ale ten byl okamžitě po jeho zveřejnění utajen. Pro jeho uvedení do praxe byla potřeba drahá výpočetní technika (tedy byl veřejně nepoužitelný).<br /> | ||
| + | |||
| + | Algoritmus byl znovu objeven v roce 1977 Ronem '''R'''ivestem, Adi '''S'''hamirem a Leonardem '''A'''dlemanem. Vznikl tak algoritmus RSA pojmenovaný podle jmen jeho tvůrců. | ||
| + | |||
| + | === Bezpečnost RSA === | ||
| + | Bezpečnost algoritmu RSA je založena za prvé na velice složitém matematickém úkonu, který se nazývá faktorizace (rozklad na prvočísla). V případě RSA jde o '''faktorizaci vysokých čísel, kdy je dešifrování zprávy v podstatě nemožné'''. RSA klíče jsou typicky dlouhé 1024-2048 bitů. Za druhé jde o RSA problém, tzn. že neznáme algoritmus dle kterého bychom mohli dešifrovat text zašifrovaný pomocí RSA. | ||
| + | === Popis činnosti RSA <ref>[http://www.kryptografie.wz.cz/data/RSA.htm Matějková, Lucie. RSA]</ref> === | ||
| + | Alice a Bob chtějí komunikovat prostřednictvím otevřeného (nezabezpečeného) kanálu a Bob by chtěl Alici poslat soukromou zprávu. | ||
| − | + | ==== Tvorba klíčového páru ==== | |
| + | '''Nejprve si bude Alice muset vyrobit pár veřejného a soukromého klíče:''' | ||
| − | + | * Zvolí dvě různá velká náhodná prvočísla p a q. | |
| − | + | * Spočítá jejich součin n = pq. | |
| − | + | * Spočítá hodnotu Eulerovy funkce φ(n) = (p − 1)(q − 1). | |
| − | + | * Zvolí celé číslo e menší než φ(n), které je s φ(n) nesoudělné. | |
| − | + | * Nalezne číslo d tak, aby platilo de ≡ 1 (mod φ(n)). | |
| − | + | * Pokud je také prvočíslo tak d = (1+r*φ(n))/e, kďe r = [(e-1)φ(n)^(e-2)] | |
| − | + | * Veřejným klíčem je dvojice (n, e), přičemž n se označuje jako modul, e jako (šifrovací, příp. 'veřejný') exponent. | |
| + | * Soukromým klíčem je dvojice (n, d), kde d se označuje jako dešifrovací či soukromý. (V praxi se klíče uchovávají v mírně upravené formě, která umožňuje rychlejší zpracování.) | ||
| − | + | Veřejný klíč poté Alice uveřejní, respektive zcela nepokrytě pošle Bobovi. Soukromý klíč naopak uchová v tajnosti. | |
| − | |||
| − | |||
| − | |||
| − | + | ==== Zašifrování zprávy ==== | |
| − | + | Bob nyní chce Alici zaslat zprávu M. Tuto zprávu převede nějakým dohodnutým postupem na číslo m (m < n). Šifrovým textem odpovídajícím této zprávě pak je číslo | |
| − | + | c = me mod n | |
| + | |||
| + | Tento šifrový text poté zašle nezabezpečeným kanálem Alici. | ||
== Bezpečnost šifer == | == Bezpečnost šifer == | ||
Pokud chceme zašifrovat nějaká data, tak nás zajímá, jak bezpečná ta šifra bude. To je ovlivněno řadou faktorů. '''Mluvíme o bezpečnostní úrovni (security level), což je měřítko síly, kterou šifra dosahuje. Běžně se vyjadřuje v bitech''' (n bitů znamená 2n operací k prolomení, jinak řečeno počet možných klíčů). | Pokud chceme zašifrovat nějaká data, tak nás zajímá, jak bezpečná ta šifra bude. To je ovlivněno řadou faktorů. '''Mluvíme o bezpečnostní úrovni (security level), což je měřítko síly, kterou šifra dosahuje. Běžně se vyjadřuje v bitech''' (n bitů znamená 2n operací k prolomení, jinak řečeno počet možných klíčů). | ||
| − | Šifrovací algoritmy mají danou pevnou délku klíče. Například DES má 56 bitů, 3DES 112 bitů, AES 128, 196 nebo 256 bitů, '''RSA 1024 nebo 2048 bitů'''. Nejkratší klíče mohou být pro symetrické algoritmy, mnohem delší jsou klíče pro asymetrické algoritmy. Speciální případ jsou eliptické křivky, které patří do asymetrických algoritmů, ale mohou mít kratší délku klíče. | + | Šifrovací algoritmy mají danou pevnou délku klíče. Například [[Data Encryption Standard|DES (Data Encryption Standard)]] má 56 bitů, 3DES 112 bitů, [[Advanced Encryption Standard|AES (Advanced Encryption Standard)]] 128, 196 nebo 256 bitů, '''RSA 1024 nebo 2048 bitů'''. Nejkratší klíče mohou být pro symetrické algoritmy, mnohem delší jsou klíče pro asymetrické algoritmy. Speciální případ jsou eliptické křivky, které patří do asymetrických algoritmů, ale mohou mít kratší délku klíče. |
== Odkazy == | == Odkazy == | ||
| Řádek 66: | Řádek 79: | ||
<references /> | <references /> | ||
| − | |||
=== Použitá literatura === | === Použitá literatura === | ||
* KINSKÝ, Jindřich. Kódování jako ochrana přenášených informací = Cryptology as a method of data protection. Praha, 2010-05-20. 56 s., 6 s. příl. Bakalářská práce (Bc.). Univerzita Karlova v Praze, Filozofická fakulta, Ústav informačních studií a knihovnictví. Vedoucí bakalářské práce Vladimír Smetáček<br /> | * KINSKÝ, Jindřich. Kódování jako ochrana přenášených informací = Cryptology as a method of data protection. Praha, 2010-05-20. 56 s., 6 s. příl. Bakalářská práce (Bc.). Univerzita Karlova v Praze, Filozofická fakulta, Ústav informačních studií a knihovnictví. Vedoucí bakalářské práce Vladimír Smetáček<br /> | ||
* Počítačové vědy. ''Informatika: Cesta do světa kryptografie''. In: ''Khan Academy'' [online]. 2021 [cit. 2021-02-19]. Dostupné z: https://cs.khanacademy.org/computing/computer-science/cryptography/crypt/v/random-vs-pseudorandom-number-generators | * Počítačové vědy. ''Informatika: Cesta do světa kryptografie''. In: ''Khan Academy'' [online]. 2021 [cit. 2021-02-19]. Dostupné z: https://cs.khanacademy.org/computing/computer-science/cryptography/crypt/v/random-vs-pseudorandom-number-generators | ||
| + | * Matějková, Lucie. ''RSA'' [online]. [cit. 2021-02-20]. Dostupné z:http://www.kryptografie.wz.cz/data/RSA.htm | ||
| + | * Algoritmus RSA. In: ''Algoritmy.net'' [online]. [cit. 2021-02-20]. Dostupné z: https://www.algoritmy.net/article/4033/RSA | ||
=== Související články === | === Související články === | ||
| Řádek 78: | Řádek 92: | ||
* [[Historický vývoj kryptografie v období světových válek]]<br /> | * [[Historický vývoj kryptografie v období světových válek]]<br /> | ||
* [[Informační bezpečnost - její klíčové aspekty, hrozby a minimalizace rizika]]<br /> | * [[Informační bezpečnost - její klíčové aspekty, hrozby a minimalizace rizika]]<br /> | ||
| + | * [[Playfair]] | ||
| + | * [[Advanced Encryption Standard]] | ||
| + | * [[Data Encryption Standard]] | ||
| + | * [[Šifry]] | ||
| + | * [[Data]] | ||
| + | * [[Digitální podpis]] | ||
| + | * [[Caesarova šifra]] | ||
| + | * [[Vernamova šifra]] | ||
| + | * [[Algoritmy kryptologie]] | ||
| + | * [[Základní rozdělení kryptologie]] | ||
| + | * [[Moderní použití kryptologie]] | ||
| + | * [[Steganografie]] | ||
| + | * [[Substituční šifry]] | ||
| + | * [[Jednoduchá monoalfabetická šifra]] | ||
| + | * [[Základní pojmy v kryptologii]] | ||
| + | * [[Historie kryptologie]] | ||
=== Klíčová slova === | === Klíčová slova === | ||
| − | + | RSA, šifrování veřejným klíčem, symetrické šifrování, asymetrické šifrování, kryptografie, bezpečnost šifer, digitální podpis | |
[[Kategorie:Informační studia a knihovnictví]] | [[Kategorie:Informační studia a knihovnictví]] | ||
[[Kategorie:Státnicové otázky UISK]] | [[Kategorie:Státnicové otázky UISK]] | ||
Aktuální verze z 23. 2. 2021, 13:49
Šifrování veřejným klíčem je metoda využívající principy asymetrického šifrování, které se od 70. let v kryptografii používá. Zásluhu na tom mají W. Diffie a M. Hellman, kteří položili základy asymetrického šifrování na základě diskrétního algoritmu.
Obsah
Kryptografie
Kryptografie je nauka o metodách utajování významu přenášených zpráv. Tato nauka je někdy nazývána jako šifrování, jelikož používá tzv. šifrování dat, což je proces, během kterého se nezabezpečená data převádí na data šifrovaná (zabezpečená), která dokáže dešifrovat jen majitel dešifrovacího klíče. Výsledný nesrozumitelný text, vzniklý pomocí šifrovacího algoritmu se nazývá šifra. Kryptografie patří společně s kryptoanalýzou (luštění šifrovaných zpráv) pod obor kryptologie.
K oboru kryptologie neoddělitelně patří pojem klíč, který v tomto případě představuje část informace, kterou si strany, které mezi sebou komunikují, vymění nějakým bezpečným kanálem. Klíč upřesňuje, jak se šifra chová. Například pokud abychom šifrovali text pomocí posouvání písmen dle abecedy, tak klíčem pak rozumíme ten počet písmen, o který se posouváme.
Používají se různé typy klíčů:[1]
- sdílený tajný klíč - zná jej více stran, používá se u symetrického šifrování
- veřejný klíč - pro zašifrování u asymetrického šifrování
- soukromý klíč - pro dešifrování u asymetrického šifrování
Důležitá je délka klíče, která je standardně určena počtem bitů. Ovlivňuje časovou náročnost při útoku hrubou silou na danou šifru, a tedy bezpečnost šifrovaných dat. Související je síla šifry. Tu stanovují kryptologové, kteří analyzují algoritmy, a hodnotí, jaké úsilí je potřeba k jejich prolomení.
Symetrické vs. asymetrické šifrování
Pod pojmem šifrování je možné si představit takovou komunikaci, kdy si dva nebo více osob posílají tajné zprávy, které lze přečíst jen pomocí zvláštního klíče, který všichni zúčastnění znají a nikdo zvenčí jej nezná (nemůže jej ani uhodnout). Takto funguje symetrická kryptografie, která k zašifrování i rozluštění zprávy používá tentýž klíč. Jak si ale účastníci tajný klíč předají? Distribuce klíčů se musí provádět na jiném principu. Šifrování zpráv navíc nemusí mít za cíl pouze udržet nějakou informaci v tajnosti, může také zajišťovat ověření totožnosti osob, např. u digitálních podpisů. Těmto účelům slouží asymetrická kryptografie, ve které se pro zašifrování používá jiný klíč než pro luštění.[2]
Symetrické šifrování
Princip symetrické metody šifrování zpráv tkví v jednom jediném klíči, který slouží k šifrování i dešifrování zpráv. Tzn. že se šifra dešifruje stejným postupem (akorát zpětným) jako byla zašifrována. Tento způsob šifrování se objevil již v dobách Julia Caesara, který používal jako princip šifrování posun o 3 písmena v abecedě. Dnes je tato metoda známá jako Caesarova šifra a je velice jednoduché ji prolomit, jelikož je zde pouze 26 možností (jako je písmen v abecedě, abychom se nedostali zpět na písmenko, které chceme šifrovat). Další symetrická šifra je tzv. Polyalfabetická šifra, která pochází z 15. století, nebo Vernamova šifra z 19. století, která jako první obsahuje princip náhody, stejně jako kdybychom házeli kostkou a hozená čísla bychom si zapisovali jako seznam náhodných posunů, který by byl následně zaslán protistraně jako společný klíč. Tato šifra se považuje za bezpečnou, jelikož se v ní posuny neopakují, nedají se předvídat a výskyt písmen je rovnoměrný.
Asymetrické šifrování
Až do 70. let 20. století bylo šifrování založeno na symetrických klíčích. Ovšem postupem času vznikla potřeba komunikovat s více lidmi (např. bankovní účty) a po zavedení internetové sítě také potřeba šifrování dvou stran, které se dohodnou na společném klíči, aniž by klíč mohl uniknout jakoukoliv cestou k nějaké třetí nezúčastněné straně. Nad tímto problémem se zamysleli W. Diffie a M. Hellman v roce 1976 a položili základy asymetrického šifrování s diskrétním algoritmem. V článku New Directions in Cryptography řešili problém distribuce klíčů a protokol, který v článku popisují se jmenuje Diffieho-Helllmanova výměna klíčů. Problém diskrétního algoritmu je v tom, že je jednoduché zprávu zašifrovat, ale dešifrovat ji zpět je velice náročné, neplatí zde princip dešifrování stejným klíčem, kterým je zpráva i zašifrována. Metoda, která obsahuje princip asymetrického šifrování se nazývá Šifrování s veřejným klíčem.
Šifrování s veřejným klíčem
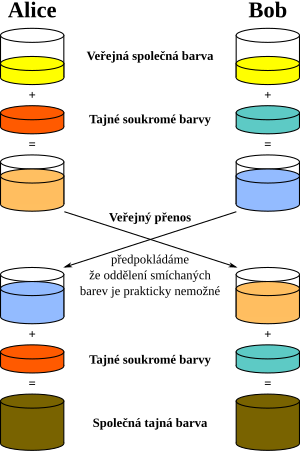
Příklad pomocí barev
Na jedné straně stojí Alice a na druhé Bob. Veřejně se dohodnou na počáteční barvě, např. žluté (tuhle barvu zná tudíž i třetí strana, která chce získat jejich komunikaci). Pak si oba náhodně zvolí svoji vlastní utajenou barvu, kterou přimíchají do žluté. Tím zamaskují jejich soukromé zprávy. Alice si nechá svoji tajnou barvu a směs pošle Bobovi (směs se dostane do rukou třetí strany). Bob si také nechá svojí tajnou barvu a směs pošle Alici (i tato směs se dostane ke třetí straně). Nyní Alice a Bob přidají své soukromé barvy do směsi toho druhého. Vznikne společná tajná barva. Třetí strana nemůže určit barvu, protože k tomu potřebuje jednu ze soukromých barev. Aby se toto dalo udělat s čísly, potřebujeme takovou číselnou operaci, která se dělá snadno v jednom směru, ale obtížně v druhém. [3]
Příklad s čísli
S barvami to zní jednoduše, pokud chceme šifrování veřejným klíčem pochopit do hloubky, tak si uvedeme i příklad s čísli. Základem šifrování klíčů je modulární aritmetika. Základní věta aritmetiky je založena na rozkládání čísla na prvočísla, všechna čísla jakkoliv velká se dají rozkládat dokud nenarazíme na prvočíslo. Jinými slovy, všechna čísla se dají vyjádřit několika prvočísly, která představují základní stavební bloky. Alice a Bob se domluví na společném klíči, který je prvočíslem (modulus) 17. Z čísla 17 máme primitivní kořen (prvočíslo) 3, kterému se říká generátor. Alice si vybere svůj tajný klíč 15 a provede výpočet gx mod p tj. 315 mod 17. Výsledkem je číslo 6, které veřejně pošle Bobovi. Bob si vybere také svůj tajný klíč 13 a provede stejný výpočet 313 mod 17. Výsledek je 12 a pošle ho veřejně zpět Alici. Alice vezme Bobův veřejný klíč 12 a umocní ho svým tajným číslem ( 1215 mod 17 = 10 ). Bob udělá to samé s Aliciným veřejným klíčem ( 613 mod 17 = 10 ). Oba získávají sdílený tajný klíč. Pokud další strana nemá privátní klíče Boba a Alice, tak se k výsledku 10 nijak nedostane, tato malá čísla byla pouze na ukázku, ale v praxi dešifrovat modulus se stovkami cifer je prakticky nemožné.
Digitální podpis
Dalším případem užití asymetrického šifrování je elektronický / digitální podpis. Používá se v případě, kdy potřebujeme podepsat důležitý dokument, který by měl nést právě náš podpis a nechceme, aby ho kdokoliv během přenosu znehodnotil, manipuloval s ním či někdo podpis zfalšoval. Chceme aby si mohl každý ověřit, že jsme podpis opravdu provedli my a nikdo jiný. Provedeme to tedy tak, že zhotovíme hash (otisk zprávy), zašifrujeme ho svým soukromým klíčem a výsledný řetězec přiložíme ke zprávě. Obojí odešleme, každý kdo bude chtít ověřit podpis a autenticitu zprávy může dešifrovat otisk pomocí našeho veřejného klíče a porovnat ho s otiskem příchozí zprávy. Pokud jsou otisky totožné, znamená to, že jsme zprávu psali my a nebylo s ní nijak manipulováno.
Metoda RSA
Jedná se o asymetrickou šifru, která je založena na Eulerově větě, a která je použitelná jak pro šifrování, tak pro podepisování dokumentů. RSA je jedním z nejrozšířenějších algoritmů na světě využívající veřejný klíč. Každý uživatel internetu používá RSA nebo jeho variantu, aniž by si to uvědomoval. Jeho síla spočívá hlavně v obtížnosti prvočíselného rozpadu.
Historie
V roce 1970 britský matematik a technik James Ellis[4] pracoval s myšlenkou neutajené šifry. Je založena na jednoduchém, a přesto chytrém konceptu. Uzamknutí a odemčení jsou inverzní operace. Bob by mohl koupit zámek, ponechat si klíč a otevřený zámek poslat Alici. Ona svoji zprávu poté uzamkne a pošle jí zpět majiteli. Vše probíhá bez výměny klíčů. To znamená, že by zámek mohl veřejně nabídnou komukoliv, aby mu díky zámku mohl poslat zprávu. Nicméně James Ellis nikdy nepřišel na matematické řešení. Jeho myšlenka je dále rozdělena na klíče dešifrovací a šifrovací. Dešifrovací klíč provádí inverzní operaci (vrací zpět operaci provedenou šifrovacím klíčem). Řešení nalezl jiný britský matematik Clifford Cocks v roce 1973.[5]Objevil ekvivalentní algoritmus k RSA, ale ten byl okamžitě po jeho zveřejnění utajen. Pro jeho uvedení do praxe byla potřeba drahá výpočetní technika (tedy byl veřejně nepoužitelný).
Algoritmus byl znovu objeven v roce 1977 Ronem Rivestem, Adi Shamirem a Leonardem Adlemanem. Vznikl tak algoritmus RSA pojmenovaný podle jmen jeho tvůrců.
Bezpečnost RSA
Bezpečnost algoritmu RSA je založena za prvé na velice složitém matematickém úkonu, který se nazývá faktorizace (rozklad na prvočísla). V případě RSA jde o faktorizaci vysokých čísel, kdy je dešifrování zprávy v podstatě nemožné. RSA klíče jsou typicky dlouhé 1024-2048 bitů. Za druhé jde o RSA problém, tzn. že neznáme algoritmus dle kterého bychom mohli dešifrovat text zašifrovaný pomocí RSA.
Popis činnosti RSA [6]
Alice a Bob chtějí komunikovat prostřednictvím otevřeného (nezabezpečeného) kanálu a Bob by chtěl Alici poslat soukromou zprávu.
Tvorba klíčového páru
Nejprve si bude Alice muset vyrobit pár veřejného a soukromého klíče:
- Zvolí dvě různá velká náhodná prvočísla p a q.
- Spočítá jejich součin n = pq.
- Spočítá hodnotu Eulerovy funkce φ(n) = (p − 1)(q − 1).
- Zvolí celé číslo e menší než φ(n), které je s φ(n) nesoudělné.
- Nalezne číslo d tak, aby platilo de ≡ 1 (mod φ(n)).
- Pokud je také prvočíslo tak d = (1+r*φ(n))/e, kďe r = [(e-1)φ(n)^(e-2)]
- Veřejným klíčem je dvojice (n, e), přičemž n se označuje jako modul, e jako (šifrovací, příp. 'veřejný') exponent.
- Soukromým klíčem je dvojice (n, d), kde d se označuje jako dešifrovací či soukromý. (V praxi se klíče uchovávají v mírně upravené formě, která umožňuje rychlejší zpracování.)
Veřejný klíč poté Alice uveřejní, respektive zcela nepokrytě pošle Bobovi. Soukromý klíč naopak uchová v tajnosti.
Zašifrování zprávy
Bob nyní chce Alici zaslat zprávu M. Tuto zprávu převede nějakým dohodnutým postupem na číslo m (m < n). Šifrovým textem odpovídajícím této zprávě pak je číslo
c = me mod n
Tento šifrový text poté zašle nezabezpečeným kanálem Alici.
Bezpečnost šifer
Pokud chceme zašifrovat nějaká data, tak nás zajímá, jak bezpečná ta šifra bude. To je ovlivněno řadou faktorů. Mluvíme o bezpečnostní úrovni (security level), což je měřítko síly, kterou šifra dosahuje. Běžně se vyjadřuje v bitech (n bitů znamená 2n operací k prolomení, jinak řečeno počet možných klíčů). Šifrovací algoritmy mají danou pevnou délku klíče. Například DES (Data Encryption Standard) má 56 bitů, 3DES 112 bitů, AES (Advanced Encryption Standard) 128, 196 nebo 256 bitů, RSA 1024 nebo 2048 bitů. Nejkratší klíče mohou být pro symetrické algoritmy, mnohem delší jsou klíče pro asymetrické algoritmy. Speciální případ jsou eliptické křivky, které patří do asymetrických algoritmů, ale mohou mít kratší délku klíče.
Odkazy
Reference
- ↑ Samuraj - Bouška, Petr, Kryptografie a šifrování
- ↑ KREJČOVÁ, Ema. Digitální peníze, 2006
- ↑ MURPHY, Dan, Cryptography in Colors: Public Key Cryptography [přednáška]
- ↑ James Ellis. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2018-05-01]. Dostupné z: https://en.wikipedia.org/wiki/James_H._Ellis
- ↑ Clifford Cocks. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2018-05-01]. Dostupné z: https://en.wikipedia.org/wiki/Clifford_Cocks
- ↑ Matějková, Lucie. RSA
Použitá literatura
- KINSKÝ, Jindřich. Kódování jako ochrana přenášených informací = Cryptology as a method of data protection. Praha, 2010-05-20. 56 s., 6 s. příl. Bakalářská práce (Bc.). Univerzita Karlova v Praze, Filozofická fakulta, Ústav informačních studií a knihovnictví. Vedoucí bakalářské práce Vladimír Smetáček
- Počítačové vědy. Informatika: Cesta do světa kryptografie. In: Khan Academy [online]. 2021 [cit. 2021-02-19]. Dostupné z: https://cs.khanacademy.org/computing/computer-science/cryptography/crypt/v/random-vs-pseudorandom-number-generators
- Matějková, Lucie. RSA [online]. [cit. 2021-02-20]. Dostupné z:http://www.kryptografie.wz.cz/data/RSA.htm
- Algoritmus RSA. In: Algoritmy.net [online]. [cit. 2021-02-20]. Dostupné z: https://www.algoritmy.net/article/4033/RSA
Související články
- Symetrická kryptografie
- Asymetrická kryptografie
- Asymetrické šifrování
- Historický vývoj kryptografie v období světových válek
- Informační bezpečnost - její klíčové aspekty, hrozby a minimalizace rizika
- Playfair
- Advanced Encryption Standard
- Data Encryption Standard
- Šifry
- Data
- Digitální podpis
- Caesarova šifra
- Vernamova šifra
- Algoritmy kryptologie
- Základní rozdělení kryptologie
- Moderní použití kryptologie
- Steganografie
- Substituční šifry
- Jednoduchá monoalfabetická šifra
- Základní pojmy v kryptologii
- Historie kryptologie
Klíčová slova
RSA, šifrování veřejným klíčem, symetrické šifrování, asymetrické šifrování, kryptografie, bezpečnost šifer, digitální podpis