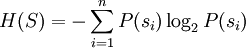Shannonovo chápání informace

Claude Elwood Shannon

Claude Elwood Shannon byl americký elektrotechnik a matematik, nazývaný též "otec teorie informace". Teorii informace, která významně ovlivnila celou řadu oborů, stvořil v Bellových laboratořích a v roce 1948 publikoval v časopise Bell System Technical Journal pod článkem "The Mathematical Theory of Communication".

Společně s Warrenem Weaverem je také autorem obecného modelu komunikace.

Shannonova definice informace: „Informace je míra množství neurčitosti nebo nejistoty o nějakém náhodném ději odstraněná realizací tohoto děje.“

Pojem BIT

Shannon zevšeobecnil myšlenky R.Hartleyho, vydané v knize "Přenos informace". Oddělil syntaktickou část od sémantické, tedy odhlédl od významu zprávy a rozdělil ji na nejmenší možné jednotky - na jednotlivé znaky. Vyjádřil přenos informace matematicky. Jednotku informace nazval binary digit (dvojková číslice), neboli zkráceně bit.

Jeden bit nese informaci odpovědi na otázku - ANO-NE; máme tedy dvě možnosti a víme, že jedna z nich je platná. Tyto možnosti lze vyjádřit čísly (1,0). Počet bitů tedy určuje, kolikrát muselo dojít k rozhodnutí, než jsme došli ke správnému výsledku.

Tento počet rozhodnutí vypočteme vzorcem:

N = sⁿ

N je počet možných zpráv, n je délka zprávy (počítáno na jednotlivé znaky), s je dvě (počet možností 1,0 - pravděpodobnost obou možností je stejná)

počet bitů vypočteme vzorcem:

I = log₂ N

1 bit je množství informace, které odstraňuje neurčitost, tedy entropii.

Entropie informace

Entropie (neuspořádanost nebo neurčitost) je základním pojmem v teorii informace. Znamená míru neurčitosti ve zprávě. Naopak informaci chápal jako odstranění této neurčitosti. Tedy s narůstající informací klesá entropie a naopak. Shannonova entropie má význam střední hodnoty.

Definoval ji takto:

"Předpokládáme existenci nějakého systému a současně předpokládáme samostatnou událost (nezávislou na předchozích událostech), která způsobí přechod systému do nového stavu. Předpokládejme n vzájemně se vylučujících stavů x, pravděpodobnost stavu i je p(i), pak entropie stavu x bude:

Míra neurčitosti nemůže být v záporných hodnotách. Znaménko minus zde znamená, že entropie je záporná veličina.

Shannon vyjádřil množství informace v jedné zprávě záporným logaritmem její pravděpodobnosti.

Shannonova entropie bodech:

"Entropie jevu se rovná nule, když je tento jev jednoznačně určený.

Entropie libovolného jevu se blíží k hodnotě nula (maximální určitosti systému), když se pravděpodobnost jevu blíží hodnotě jedna nebo nula.

Entropie je kladné číslo, v krajním případě (pro P=1 nebo P=0) rovné 0.

Entropie je maximální, při rovnoměrném rozložení pravděpodobnosti všech možných jevů.

Entropie složeného pokusu, v kterém záleží na pořadí pokusů a kde jsou jevy navzájem nezávislé, je celková entropie rovna součtu entropií jednotlivých pokusů."

Literatura

Průkopníci informačního věku (10.): Claude Shannon. CIO Business World [online]. 2010, č. 11 [cit. 2015-01-24]. Dostupné z: http://businessworld.cz/cio-bw-special/prukopnici-informacniho-veku-10-claude-shannon-6969